Question
Using l'Hopital's rule, show (this can be quite tricky) that T (xj) lim L(x)= = x-xj 2T'(xj) Given T+1(x) = cos((n + 1) cos
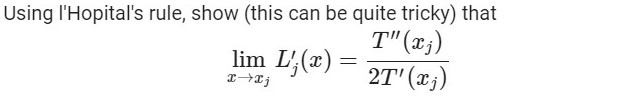
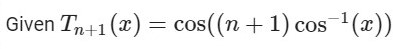
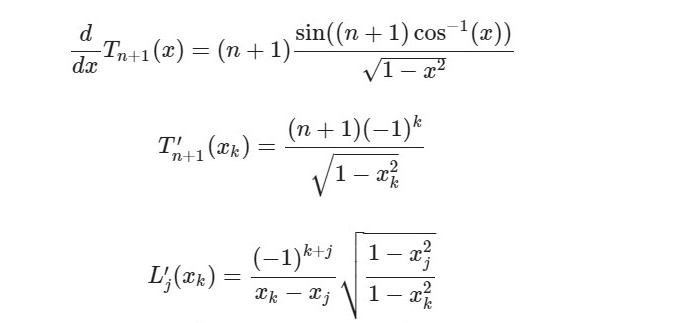
Using l'Hopital's rule, show (this can be quite tricky) that T" (xj) lim L(x)= = x-xj 2T'(xj) Given T+1(x) = cos((n + 1) cos (x)) d dx sin((n + 1) cos(x)) Tn+1(2) = = (n + 1). T+1(k) = 1-x2 (n + 1)(1)k = 1 - x/ (1)k+j 1 - x L'(x)= = xk - 1 - x
Step by Step Solution
There are 3 Steps involved in it
Step: 1
To use LHpitals rule to find the limit limx Lx we first ...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get StartedRecommended Textbook for
International Finance Putting Theory Into Practice
Authors: Piet Sercu
1st edition
069113667X, 978-0691136677
Students also viewed these Mathematics questions
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
Question
Answered: 1 week ago
View Answer in SolutionInn App



