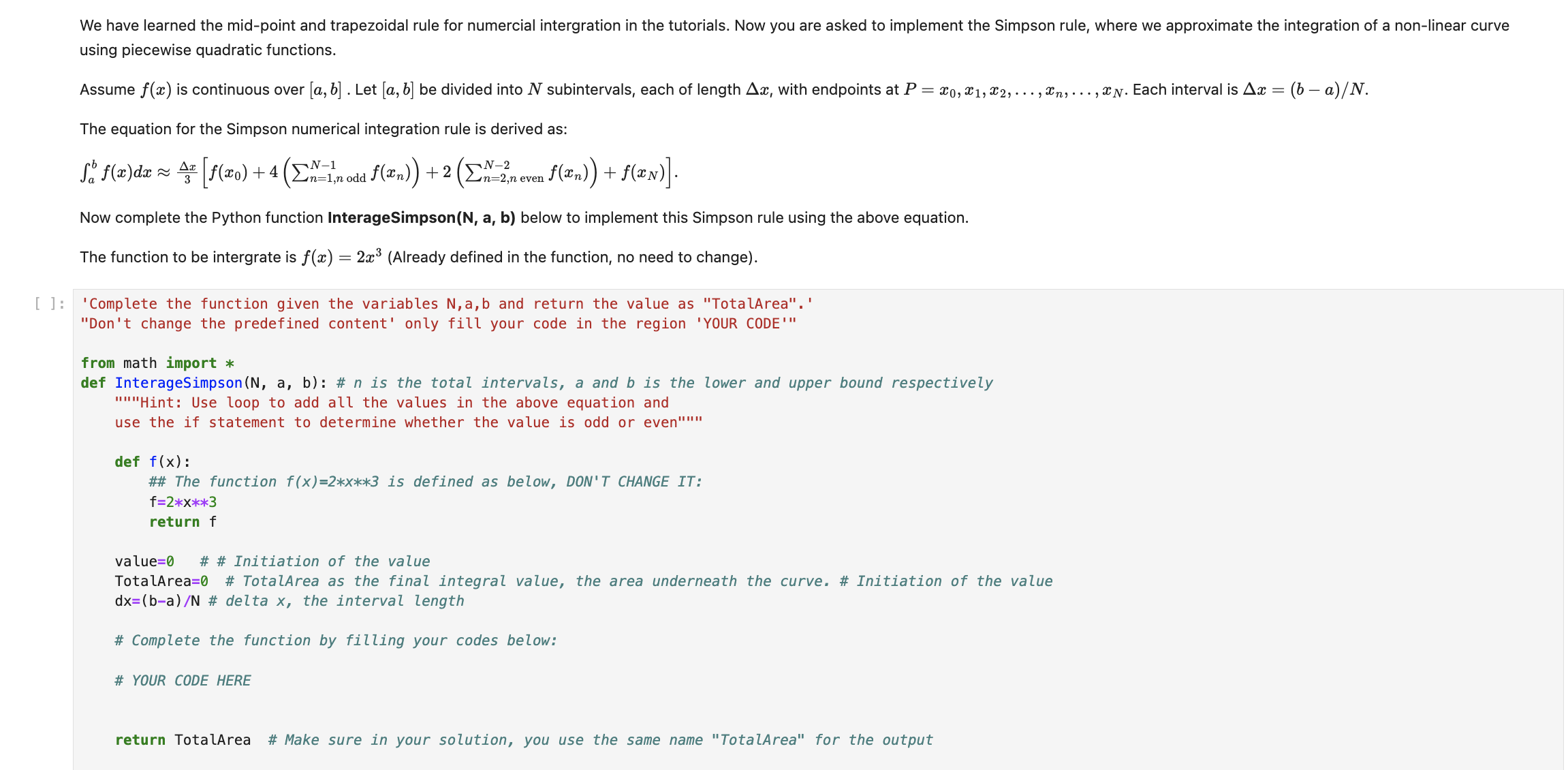
Question
using piecewise quadratic functions. Assume f(x) is continuous over a,b . Let a,b be divided into N subintervals, each of length Delta x , with
using piecewise quadratic functions.\ Assume
f(x)is continuous over
a,b. Let
a,bbe divided into
Nsubintervals, each of length
\\\\Delta x, with endpoints at
P=x_(0),x_(1),x_(2),dots,x_(n),dots,x_(N). Each interval is
\\\\Delta x=(b-a)/(N).\ The equation for the Simpson numerical integration rule is derived as:\
\\\\int_a^b f(x)dx~~(\\\\Delta x)/(3)[f(x_(0))+4(\\\\sum_(n=1)^(N-1) ,n odd f(x_(n)))+2(\\\\sum_(n=2)^(N-2) ,n even f(x_(n)))+f(x_(N))].\ Now complete the Python function InterageSimpson(N, a, b) below to implement this Simpson rule using the above equation.\ The function to be intergrate is
f(x)=2x^(3)(Already defined in the function, no need to change).\ from math import
**\ def InterageSimpson(
N,a,b#
nis the total intervals,
aand
bis the lower and upper bound respectively\ "'"'Hint: Use loop to add all the values in the above equation and\ use the if statement to determine whether the value is odd or even"'"."\ def
f(x):\ ## The function
f(x)=2**x****3is defined as below, DON'T CHANGE IT:\
f=2**x****3\
return f\ value
=0# # Initiation of the value\ TotalArea=0 # TotalArea as the final integral value, the area underneath the curve. # Initiation of the value\
dx=(b-a)/(N)#delta
x, the interval length\ # Complete the function by filling your codes below:\ # YOUR CODE HERE
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


