Using STRONG INDUCTION please solve the following question and its follow up questions

In this question you will be asked to analyze the game described below:

Begin with a pile of n stones and a score of 0 points. In the first move, split the pile into two possibly unequal sub-piles, multiply the number of stones in one sub-pile by the number of stones in the other sub-pile and add that product to the score. Continue by successively splitting each newly created pile of stones that has at least two stones into a pair of sub-piles which are not necessarily the same size. Each time you split a pile into two sub-piles, multiply the number of stones in one of these sub-pile by the number of stones in the other sub-pile and add that product to the score. Continue the game until there are n piles of 1 stone each. The score at that point is the final score for the game.

Define G(n) to be the final score of the game when it played with n stones.

You will use strong induction to prove that 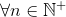G(n)= n(n-1)/2

a. Symbolic form - Your conjecture has already been stated in symbolic form. It is a statement of the form 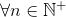, P(n) . What is the predicate function P(n)?

b. Proof: Setup Base case ?

c. Proof: Inductive step setup, state your assumption and Inductive Hypothesis (This is the beginning of the inductive step where you are stating the assumption in the inductive step and what you will be proving in that step. As you do so, identify the inductive hypothesis)

d. Proof: Inductive step

Please answer everything in bold.

+ NUA + NUA + NUA + NUA