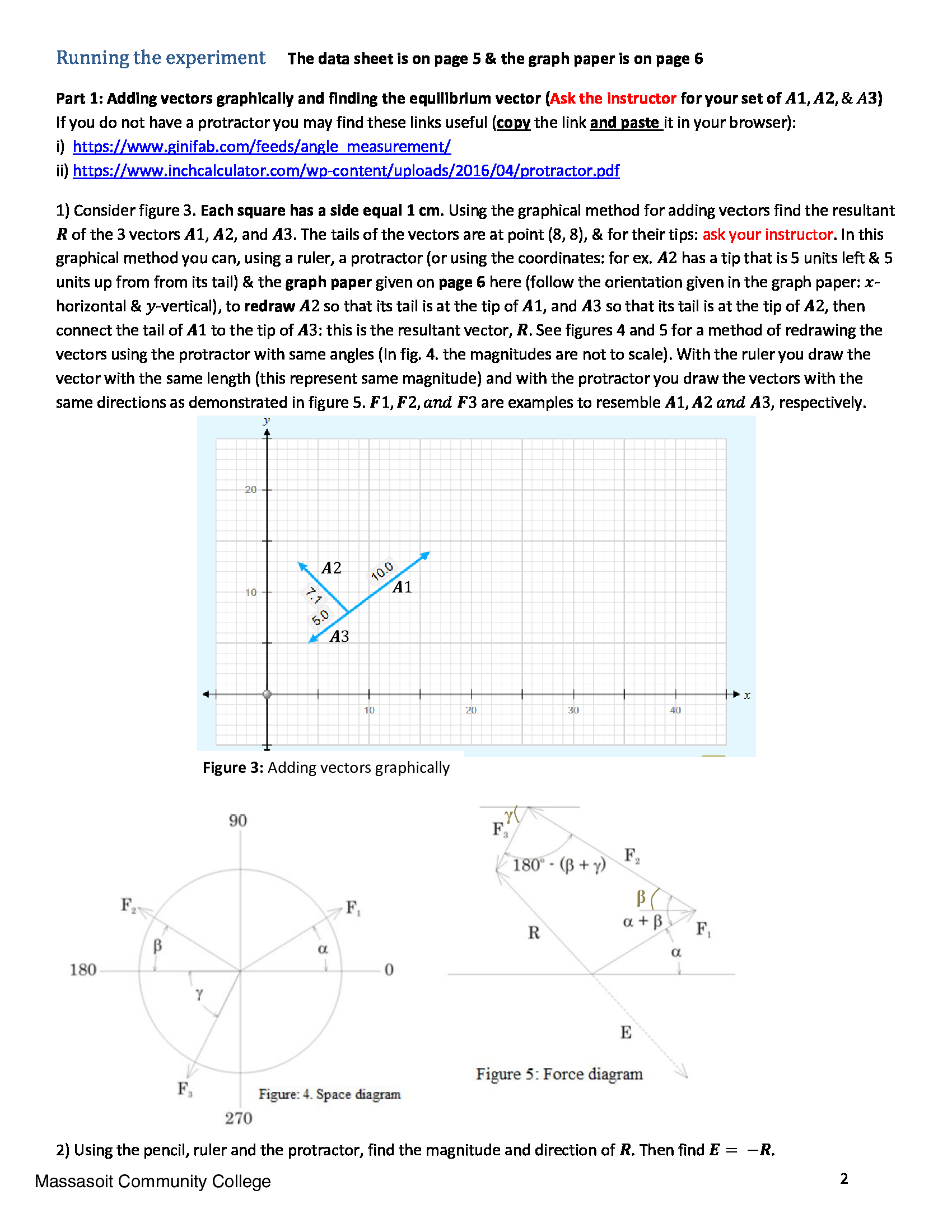
Vectors Purpose 1. To study vectors and their addition graphically. 2. To study resolution of a two dimensional vector and the addition method through components. Introduction Vectors are quantities that have both direction and magnitude. The magnitude is the numerical value of the vector. A quantity that has only magnitude (no direction) is called a scalar. A scalar could have any value including negative values, but it does not have a direction. Examples of scalars are temperature, distance and mass. Examples of vectors are force, velocity and acceleration. The direction of a force vector, is the direction in which the force is applied. The magnitude of the force vector is the strength of the force. We draw vectors as ray with the direction as the arrow. When drawing a vector we represent the magnitude of a vector by the length of that vector. 50 a strong force is represented by a longer vector than a weak force. As a notation, we will write a vector in bold 'A', while its magnitude in normal font 'A'. Part 1: Adding vectors When we add vectors we have to take the direction of the vector into consideration. Two equal but opposite vectors add up to zero. Since a vector is characterized by only magnitude (represented by length of the vector) and direction, then we if we move the vector parallel to itself while keeping its length fixed, we still have the same vector (since in moving the vector parallel to itself we preserved its direction and magnitude). A method to add vectors is to arrange them in a way that the tip of the 1St vector is at the tail of the 2"'1 vector and the tip of the 2"d vector is at the tail of the 3"d vector and so on. Then the sum of the vectors, called Resultant vector, R, is a vector that connects the tail of the 1't vector to the tip of the last vector. See figure 1. R = A1 + A2 + A3. If a A3 vectorE is equal and opposite to R (E = R), then E + R = 0. E is called A2 A2 the 'equilibrant vector'. If the vectors represent forces, then E is the force 3 /A1 (2:) Rll that when added to the other force vectors will produce equilibrium. A3 Al Part 2: Resolving a vector Figure 1: Adding vectors graphically Consider the Mo vectors Ax (horizontal) and A31 (vertical) in Figure 2. If we add the vectors Ax and Ay using the graphical addition method above, we get the Resultant vector. We will call it A here. 50, A = Ax + Ay. So in a plane, any vectorA can be analyzed (resolved) to two components a horizontal component Ax and a vertical component Ay. Using trigonometry, Ax = A0056 andAy = Asin eqns. (1) A