Question: Verify that the vector X is a solution of the given coupled system of the initial value problem. dx dy dt dt where X(0) =

Verify that the vector X is a solution of the given coupled system of the initial value problem.
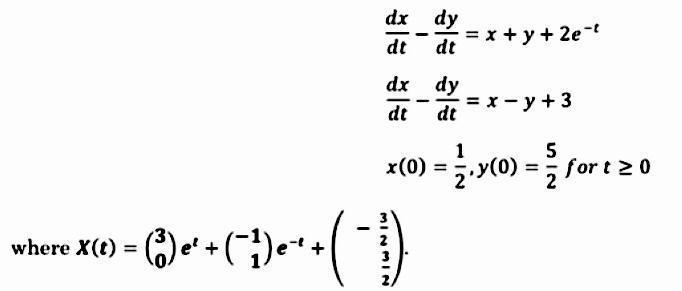
$( begin{array}{c}frac{d x}{d t}-frac{d y}{d t}=x+y+2 e^{-t} frac{d x}{d t}-frac{d y}{d t}=x-y+3 x(0)=frac{1}{2},$

dx dy dt dt where X(0) = (3) e + (`)e ^ + ( dx dy dt dt I ( _ - _) MINMIN - = x+y+2e-t 5 x(0) = 1, y(0) = { for t 0 2 = x=y+3

Step by Step Solution

★★★★★

3.38 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Tiven the vector Xt 3 e 1 et 32 t xt 3et 32 and x0 3 32 and y0 1 32 t Yt 32 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Suppose X and Y have constant density on the region in Figure 26.2. a. Are X and Y independent? b. Find P{X + Y

In Exercises determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. 1 1/ 4x = dx = [ 1n/x1] = - 1 In 2 In 1 In 2

Apply the methods of this and the previous section to graph each function. Be sure to label key points and show at least two periods. y = -cot 2x + 2

Verify that if c is a constant, then the function defined piecewise by satisfies the differential equation y' = 3y 2/3 for all x. Can you also use the "left half" of the cubic y = (x - c) 3 in...

Apply the iterative formula in (16) to compute the first three successive approximations to the solution of the initial value problem dx dt dy dt = 2x - y, = 3x - 2y, x(0) = 1; y(0) = -1.

If c 0, verify that the function defined by y(x) x/(cx - 1) (with the graph illustrated in Fig. 1.3.26) sat- isfies the differential equation x 2 y' + y 2 = 0 if x 1/c. Sketch a variety of such...

Solve the differential equation (dy/dx) 2 = 4y to verify the general solution curves and singular solution curve that are illustrated in Fig. 1.4.5. Then determine the points (a, b) in the plane for...

In Problems 21 and 22, first use the method of Example 2 to construct a slope field for the given differential equation. Then sketch the solution curve corresponding to the given initial condition....

Reread Example 3 and then discuss, with reference to Theorem 1.2.1, the existence and uniqueness of a solution of the initial-value problem consisting of xy' - 4y = x 6 e x and the given initial...

The solution to the initial value problem for the diffusion equation is unique (given certain constraints on the behavior, it must be sufficiently smooth and decay sufficiently fast at infinity)....

Suppose the graph of a cubic polynomial intersects the parabola y = x2 when x = 0, x = a, and x = b, where 0

On January 1, 2011, Q-Mart entered into a five-year lease agreement requiring annual payments of $10,000 on December 31 of each year. The fair market value of the facility was estimated by appraisers...

Chev Limited, a software development company, is considering acquiring Polo Limited through a share exchange. The proposed merger is expected to generate economies of scale, resulting in an estimated...

1 point) Determine whether the three points P= (6, -9, -9), Q = (8, 5, -3), R= (10, 1,3) are collinear by computing the distances between pairs of points istance from P to Q istance from Q to R...

(1 point) Find a unit vector with positive first coordinate that is orthogonal to the plane through the points P=(4,3, 4), Q(3, 4, 3), and R= (3, 4, -1). Note: You can earn partial credit on this...

(1 point) (A) Find the parametric equations for the line through the point P = (4, -5, 1) that is perpendicular to the plane -5r + ly + 1z = 1. Use "" as your variable, t= 0 should correspond to P,...

(1 point) Find an equation of a plane through the point (-5, -4, 2) which is orthogonal to the line * =1+ 2t, y = -1 lt, z=-5+ 4t in which the coefficient of z is 2. Equation: = 0

The _____ selection strategy involves rank order applicants' scores from highest to lowest and extend job offers to applicants at the top of the list and move to the bottom.Group of answer...

The equation of motion for a damped simple harmonic oscillator is ?where k and ? are constants, m is the mass and x is the displacement of the system. Describe the conditions for lightly damped,...

Verify that the vector X is a solution of the given homogeneous linear system. dx _- 2x + 5y dt dy -2x + 4y; X = 5 cos(t) 3 cos(t) - sin(t) et dt Writing the system in the form X' = AX for some...

Verify that the vector X is a solution of the given homogeneous system 1 3 3 For X 133 4 one has X 0X Since the above expressions X Select 133 X 13 133 3 is a solution of the given syste

(1) (2 points) Let A, B denote m x n matrices. Explain why A = B iff Ax = Bx holds for all n-dimensional column vectors x in R". (2) (3 points) The vectors are a basis (which we HOW denote by B) for...

Verify that the vector X is a solution of the given system. X' = ( 2 X; X = et te 4

Verify that the vector X is a solution of the given system. 1 1' 0 X; X = -2 -1 X' = 6 -1 6 -13, 2.