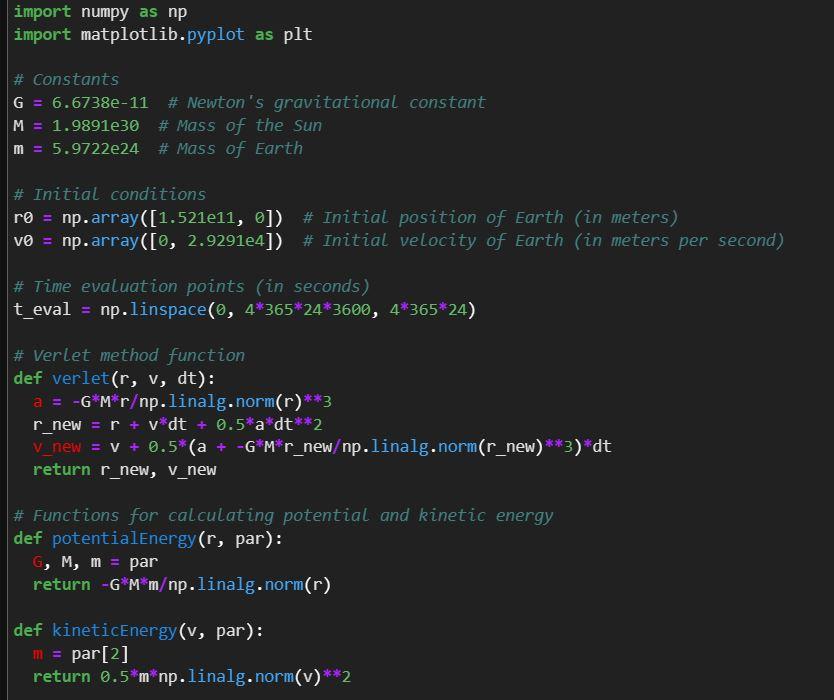
Verlet Method

Here is what I have tried but I can't find the mistake

Thanks!

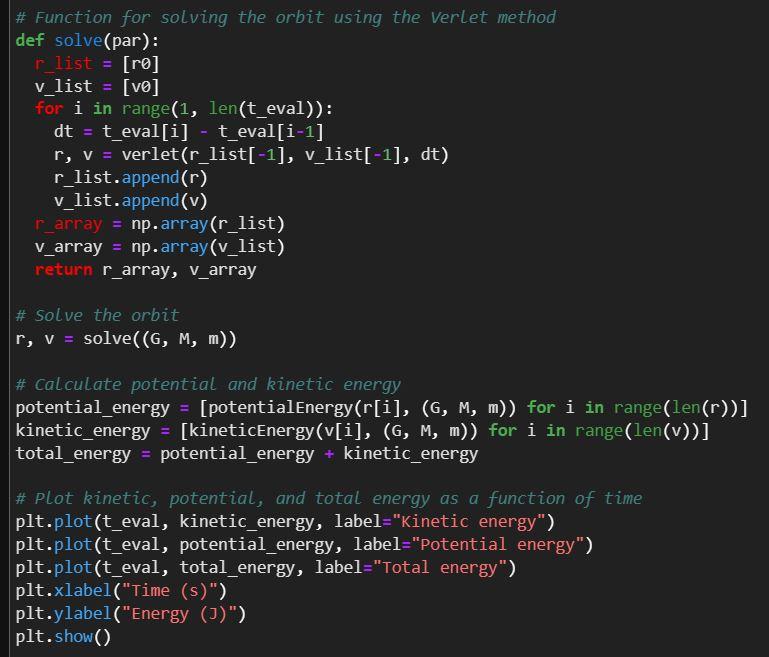
dt2d2x(t)=GMr3x,dt2d2y(t)=GMr3y, where r=x2+y2 Task: Calculate the orbit of the Earth around the Sun in steps of one hour for a total period of four years. Use the solution for the orbit, r(t), and the velocity, v(t), to calculate additionally the potential and kinetic energy of Earth at each evaluation point. Create a function potentialEnergy( r, par) and a function kineticEnergy( v, par) which implement these requested calculations separately from solving the ODE's and can be called from tests. Also create a function solve(par) which returns the value arrays for r(t) and v(t) as a tuple such that the tests can call solve(par) and obtain the results. Note that the potential energy depends only on the Earth location, r(t), and its kinetic energy only on its velocity, v(t). The variable par should be a tuple containing the required constant values in order (G,M,m), see Data below. Data: Use G=6.67381011m3kg1s2 as Newton's gravitational constant, M=1.98911030kg as mass of the Sun. For Earth mass, use m=5.97221024kg. The initial conditions should be r0=(1.5211011,0)m and v0=(0,2.9291104)ms1. Time evaluation points are in the task description and note that you work in SI units. Create two plots: (a) draw the kinetic energy, potential energy and total energy, superimposed on a single canvas and observe how the kinetic and potential energies change as a function of time while the total energy appears to be constant. (b) Plot only the total energy as a function of time and observe the oscillating character while the mean remains constant to high precision which demonstrates the inherent energy conservation of the Verlet method. Note: you may wish to solve the problem using solve_ivp() but that is not recommended. It is entirely possible and possibly illuminating in comparison(!) to the Verlet method but effectively similar effort for worse results. The tests are likely to fail and deduct marks for this case. def solve(par): r_list = [ro] v_list = [v0] for i in range(1, len(t_eval)): dt = t_eval[i] - t_eval[i-1] r, v = verlet(r_list[-1], v_list[-1], dt) r_list.append(r) v_list.append(v) r_array = np.array(r_list) v_array = np.array(v_list) return r_array, v_array \# solve the orbit r, v = solve((G, M, m)) \# calculate potential and kinetic energy potential_energy = [potentialenergy(r[i], (G, M, m)) for i in range(len(r))] kinetic_energy = [kineticEnergy(v[i], (G, M, m)) for i in range(len(v))] total_energy = potential_energy + kinetic_energy \# Plot kinetic, potential, and total energy as a function of time plt.plot(t_eval, kinetic_energy, label="Kinetic energy") plt.plot(t_eval, potential_energy, label="Potential energy") plt.plot(t_eval, total_energy, label="Total energy") plt.xlabel("Time (s)") plt.ylabel("Energy ( J)") plt.show()