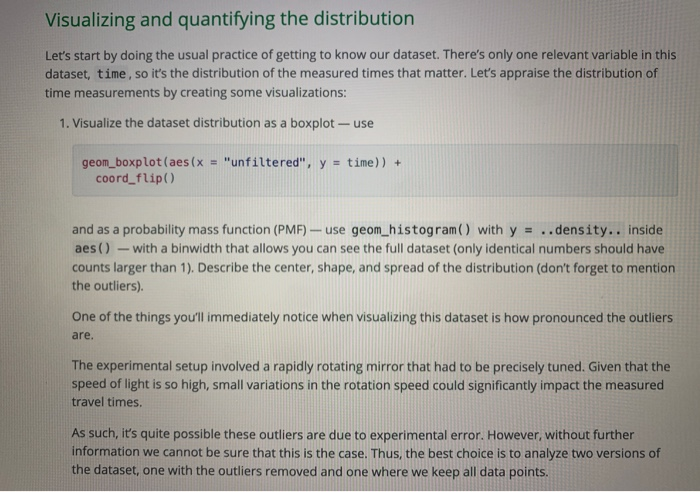
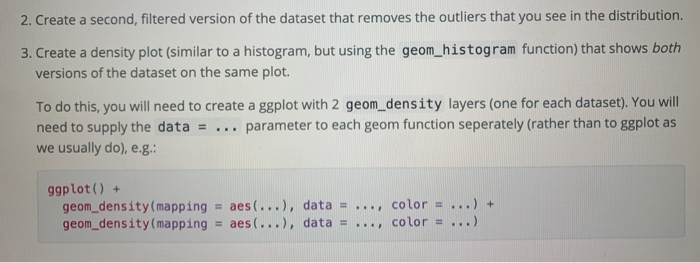
Visualizing and quantifying the distribution Let's start by doing the usual practice of getting to know our dataset. There's only one relevant variable in this dataset, time, so it's the distribution of the measured times that matter. Let's appraise the distribution of time measurements by creating some visualizations: 1. Visualize the dataset distribution as a boxplot -- use geom_boxplot(aes(x = "unfiltered", y = time)) + coord_flip) and as a probability mass function (PMF) - use geom_histogram() with y = ..density.. inside aes() - with a binwidth that allows you can see the full dataset (only identical numbers should have counts larger than 1). Describe the center, shape, and spread of the distribution (don't forget to mention the outliers). One of the things you'll immediately notice when visualizing this dataset is how pronounced the outliers are. The experimental setup involved a rapidly rotating mirror that had to be precisely tuned. Given that the speed of light is so high, small variations in the rotation speed could significantly impact the measured travel times. As such, it's quite possible these outliers are due to experimental error. However, without further information we cannot be sure that this is the case. Thus, the best choice is to analyze two versions of the dataset, one with the outliers removed and one where we keep all data points. 2. Create a second, filtered version of the dataset that removes the outliers that you see in the distribution. 3. Create a density plot (similar to a histogram, but using the geom_histogram function) that shows both versions of the dataset on the same plot. To do this, you will need to create a ggplot with 2 geom_density layers (one for each dataset). You will need to supply the data = ... parameter to each geom function seperately (rather than to ggplot as we usually do), e.g.: ggplot() + geom_density(mapping = aes(...), data = ..., color = ...) + geom_density (mapping = aes (...), data = ..., color = ...) Visualizing and quantifying the distribution Let's start by doing the usual practice of getting to know our dataset. There's only one relevant variable in this dataset, time, so it's the distribution of the measured times that matter. Let's appraise the distribution of time measurements by creating some visualizations: 1. Visualize the dataset distribution as a boxplot -- use geom_boxplot(aes(x = "unfiltered", y = time)) + coord_flip) and as a probability mass function (PMF) - use geom_histogram() with y = ..density.. inside aes() - with a binwidth that allows you can see the full dataset (only identical numbers should have counts larger than 1). Describe the center, shape, and spread of the distribution (don't forget to mention the outliers). One of the things you'll immediately notice when visualizing this dataset is how pronounced the outliers are. The experimental setup involved a rapidly rotating mirror that had to be precisely tuned. Given that the speed of light is so high, small variations in the rotation speed could significantly impact the measured travel times. As such, it's quite possible these outliers are due to experimental error. However, without further information we cannot be sure that this is the case. Thus, the best choice is to analyze two versions of the dataset, one with the outliers removed and one where we keep all data points. 2. Create a second, filtered version of the dataset that removes the outliers that you see in the distribution. 3. Create a density plot (similar to a histogram, but using the geom_histogram function) that shows both versions of the dataset on the same plot. To do this, you will need to create a ggplot with 2 geom_density layers (one for each dataset). You will need to supply the data = ... parameter to each geom function seperately (rather than to ggplot as we usually do), e.g.: ggplot() + geom_density(mapping = aes(...), data = ..., color = ...) + geom_density (mapping = aes (...), data = ..., color = ...)