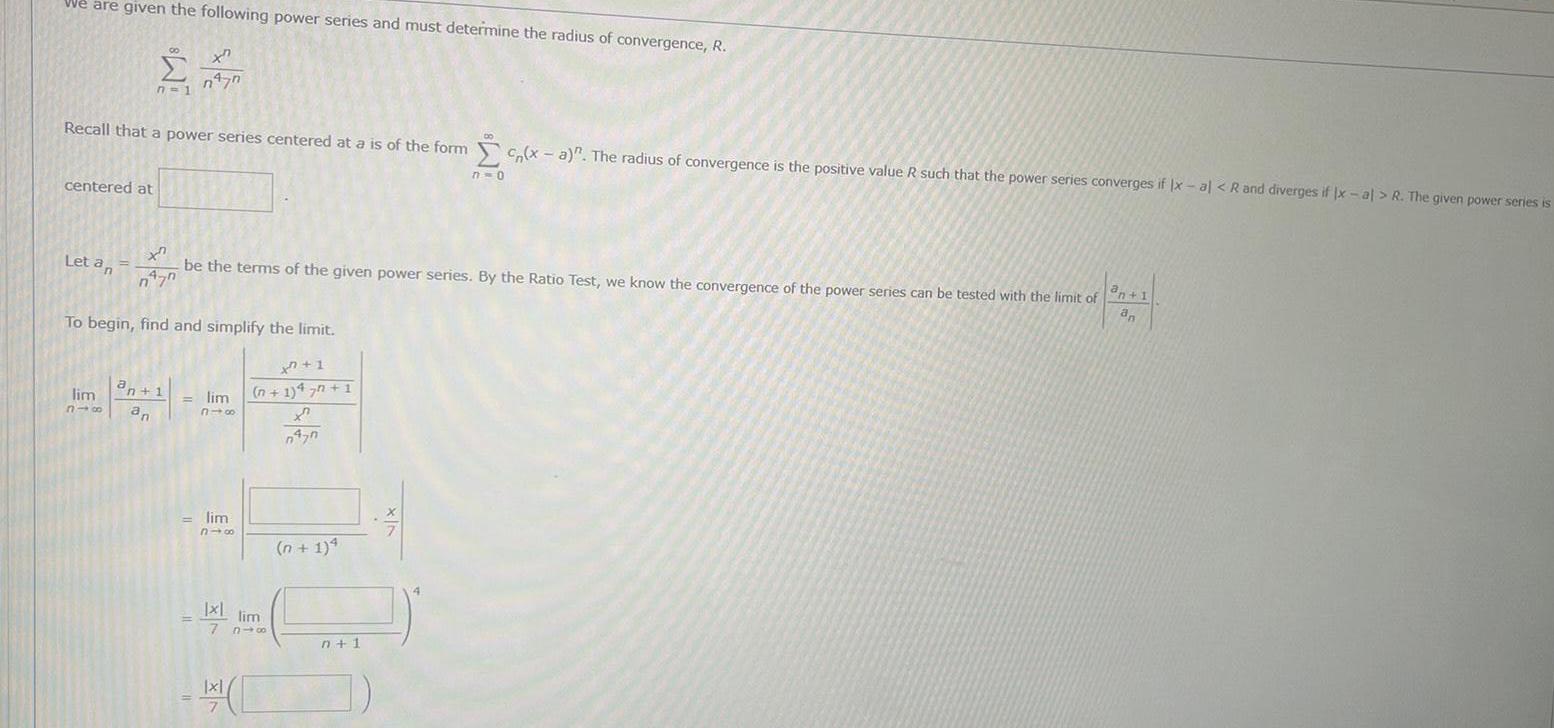
We are given the following power series and must determine the radius of convergence, R. n=1 . Recall that a power series centered at a is of the form (x - a)". The radius of convergence is the positive value R such that the power series converges if lx-a] < R and diverges if lx - al > R. The given power series is centered at 7-0 Let an an be the terms of the given power series. By the Ratio Test, we know the convergence of the power series can be tested with the limit of n+1 n7n To begin, find and simplify the limit. lim 319 an+1 an lim +7+1 (n+1)4 7+1 818 = lim 818 (n+1)4 1x lim 7 n n+1 |x|