We are interested in measuring the time complexity of executing a sequence of n invocations of the following function with the array A initially containing all 0's. Function increment(A) Input: A[0..m-1] is an array of 0-1 bits representing a binary counter Output: A after its value incremented by 1 modulo 2m i 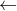0 while i do A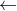[i] 0 i 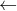i + 1 end if i then A[i] 1 end (a) Note the time complexity of the function is proportional to number of itera- tions of the while loop and can be O(m) in the worst case. Thus concluding that the sequence of n invocations takes O(mn) time is incorrect as it is a loose bound. We can use amortized complexity analysis to improve the bound. Using accounting method show that the amortized complexity of a single invocation in a sequence of n invocations is O(1). [Hint : Assume cost of a function is measured by number of bit ips(0 to 1 and 1 to 0) required. Argue that the amortized cost is 2 units per invocation]

(b) What potential function will you use for the amortized analysis ? Derive the amortized time complexity using this potential function.

We are interested in measuring the time complexity of executing a sequence of n invocations of the following function with the array A initially containing all 0's. Function increment (A) Input: A[0.m-1 is an array of 0-1 bits representing a binary counter Output: A after its value incremented by 1 modulo 2 i-0 while i