We have an unsorted array of integers and we want to find the value of an element at index k that would be there if the array was sorted.

The simplest way to find the k^th element is to sort the data and take the value that is at the index k. But sorting does more than necessary to solve this problem. You need to find only the k^th smallest entry in the collection for an appropriate value of k. We can use the partitioning strategy of quick sort to find the k^th smallest entry in the array:

After choosing a pivot and forming the sub-arrays Smaller and Larger

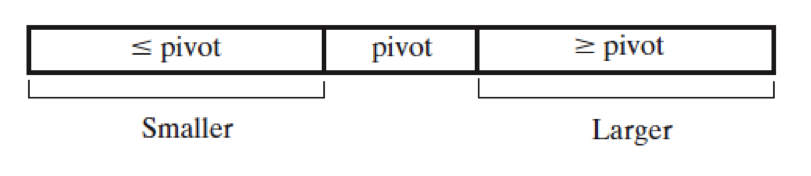
you can draw one of the following three conclusions:

if pivot index is the same as k, the k^th smallest element is the entry at the pivot index

if Smaller sub-array contains k or more entries, it must contain the k^th smallest entry

otherwise the k^thelement is in Larger sub-array

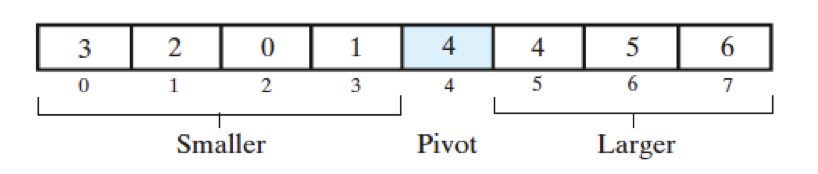
For example, let us assume that we are looking for the smallest entry that would be at index 3 if the array was sorted. The initial array is: 3 5 0 4 6 1 2 4 . After the first partition it will look as follow:

1.develop a recursive algorithm to find the k^th smallest entry. The conclusion 1) represents the base case, conclusions 2) and 3) represent recursive calls.

2.implement the recursive kthItem method that is already defined in the KthElement.java. Your method should call partition(a, first, last) method to get the pivotIndex

3.run main to test your code

ONLY need to Complete //TODO!!!

public class KthElement { /**  * Task: Sorts the first, middle, and last elements of an  * array into ascending order.  *  * @param a an array of Comparable objects  * @param first the integer index of the first array element; first >= 0  * @param mid the integer index of the middle array element  * @param last the integer index of the last array element;  * last - first >= 2, last  */  private static > void sortFirstMiddleLast(T[] a, int first, int mid, int last) { orderTwoItems(a, first, mid); // make a[first] orderTwoItems(a, mid, last); // make a[mid] orderTwoItems(a, first, mid); // make a[first] /**  * Task: Orders two given array elements into ascending order  * so that a[i]  *  * @param a an array of Comparable objects  * @param i an integer >= 0 and  * @param j an integer >= 0 and  */  private static > void orderTwoItems(T[] a, int i, int j) { if (a[i].compareTo(a[j]) > 0) swap(a, i, j); } // end orderToItems /**  * Task: Swaps the array elements a[i] and a[j].  *  * @param a an array of objects  * @param i an integer >= 0 and  * @param j an integer >= 0 and  * assumes that i != j  */  private static  void swap(T[] a, int i, int j) { T temp = a[i]; a[i] = a[j]; a[j] = temp; } // end swap /**  * Task: Partitions an array as part of quick sort into two subarrays  * called Smaller and Larger that are separated by a single  * element called the pivot.  * Elements in Smaller are left of the pivot and  * Elements in Larger are right of the pivot and >= pivot.  *  * @param a an array of Comparable objects  * @param first the integer index of the first array element;  * first >= 0  * @param last the integer index of the last array element;  * last >= first; last  * @return the index of the pivot  */  private static > int partition(T[] a, int first, int last) { int mid = first + (last - first) / 2; sortFirstMiddleLast(a, first, mid, last); int pivotIndex = mid; if (last - first + 1 > 3) { // Assertion: The pivot is a[mid]; a[first] = pivot, so do not compare these two array entries // with pivot. // Move pivot to next-to-last position in array swap(a, mid, last - 1); pivotIndex = last - 1; T pivotValue = a[pivotIndex]; // Determine subarrays Smaller = a[first..endSmaller] // and Larger = a[endSmaller+1..last-1] // such that entries in Smaller are = pivotValue; initially, these subarrays are empty int indexFromLeft = first + 1; int indexFromRight = last - 2; boolean done = false; while (!done) { // Starting at beginning of array, leave entries that are = pivotValue; you will find one, // since last entry is >= pivot while (a[indexFromLeft].compareTo(pivotValue)  pivot; // locate first entry that is  0) indexFromRight--; assert a[indexFromLeft].compareTo(pivotValue) >= 0 && a[indexFromRight].compareTo(pivotValue) swap(a, indexFromLeft, indexFromRight); indexFromLeft++; indexFromRight--; } else done = true; } // Place pivotValue between the subarrays Smaller and Larger swap(a, pivotIndex, indexFromLeft); pivotIndex = indexFromLeft; // Assertion: // Smaller = a[first..pivotIndex-1] // Pivot = a[pivotIndex] // Larger = a[pivotIndex+1..last] } return pivotIndex; } // end partition /**************************************************************  * KTH ORDER STATISTIC - ALGORITHM THAT USES PARTITION  * ARRAY MAY BE SORTED OR UNSORTED  **************************************************************/   /**  * Task: Find the kth item of the first n items in sorted order  *  * @param a an array of Comparable objects  * @param n an integer >= 0 and less than or equal to a.length  * @param k an integer >= 0 and less than or equal to n  */  public static > T kthItem(T[] a, int k, int n) { return kthItem(a, k, 0, n - 1); } // end kthItem /**  * Recursively finds the kth item in a array of items  * utilizing partitioning strategy of quick sort.  *  * @param a an array of Comparable objects  * @param k an integer >= 0 that is the position of the item to return.  * @param first an integer >= 0 that is the index of the first  * array element to consider  * @param last an integer >= 0 that is the index of the last  * array element to consider  */  private static > T kthItem(T[] a, int k, int first, int last) { //TODO Project1   //System.out.println("call: " + k + " " + first + " " + last + " "); // IMPLEMENT kthItem METHOD RECURSIVELY // HINT: call partition(a, first, last) method to get the pivotIndex return null; //THIS IS A STUB } // end kthItem public static int getNextPrime(int integer) { // if even, add 1 to make odd if (integer % 2 == 0) { integer++; } // test odd integers while (!isPrime(integer)) { integer = integer + 2; } return integer; } // end getNextPrime private static boolean isPrime(int integer) { boolean result; boolean done = false; // 1 and even numbers are not prime if ((integer == 1) || (integer % 2 == 0)) { result = false; } // 2 and 3 are prime else if ((integer == 2) || (integer == 3)) { result = true; } else // integer is odd and >= 5 { assert (integer % 2 != 0) && (integer >= 5); // a prime is odd and not divisible by every odd integer up to its square root result = true; // assume prime for (int divisor = 3; !done && (divisor * divisor in); System.out.println("What size array should be used?" + " It should be an integer value greater than or equal to 1."); arraySize = keyboard.nextInt(); System.out.println("How many arrays should be used (number of trials)?" + " It should be an integer value greater than or equal to 1."); trials = keyboard.nextInt(); System.out.println("What seed should be used?" + " It should be an integer value greater than or equal to 1."); seed = keyboard.nextInt(); } catch (InputMismatchException ime) { System.out.println("Could not convert input to an integer"); invalidInput = true; } catch (Exception e) { System.out.println("There was an error with System.in"); System.out.println(e.getMessage()); invalidInput = true; } } while (invalidInput); // start testing Integer data[]; Integer forTesting[]; for (int i = 1; i out.println(" TRIAL #" + i); Random generator = new Random(seed); // create an array and fill it with random values between 0 and MAX_RANDOM exclusive data = new Integer[arraySize]; for (int j = 0; j out.println("The original array is: "); System.out.println(Arrays.toString(data)); // make a copy of the original array we will sort it and use it for comparing result forTesting = Arrays.copyOf(data, arraySize); Arrays.sort(forTesting); System.out.println("The original array sorted would be: "); System.out.println(Arrays.toString(forTesting)); boolean failed = false; for (int k = 0; k kthItem(data, k, arraySize); // we want to test the code as much as possible but the following case is what we want to print if (k == (arraySize / 2)) { System.out.println(">>> kthItem found median at index " + k + " with value of " + result + " out.println(" fails - item at k equal to " + k + " is : " + forTesting[k] + " got " + result + " instead"); } } if (!failed) System.out.println(" passes"); seed = getNextPrime(++seed); } } }

See the sample run:

What size array should be used?

It should be an integer value greater than or equal to 1.

21

How many arrays should be used (number of trials)?

It should be an integer value greater than or equal to 1.

3

What seed should be used?

It should be an integer value greater than or equal to 1.

11

TRIAL #1

The original array is:

[38, 68, 11, 55, 33, 7, 40, 33, 93, 7, 14, 94, 87, 9, 62, 18, 94, 91, 28, 6, 25]

The original array sorted would be:

[6, 7, 7, 9, 11, 14, 18, 25, 28, 33, 33, 38, 40, 55, 62, 68, 87, 91, 93, 94, 94]

>>> kthItem found median at index 10 with value of 33

passes

TRIAL #2

The original array is:

[92, 0, 75, 98, 63, 10, 93, 13, 56, 14, 60, 16, 5, 55, 62, 54, 44, 69, 60, 24, 23]

The original array sorted would be:

[0, 5, 10, 13, 14, 16, 23, 24, 44, 54, 55, 56, 60, 60, 62, 63, 69, 75, 92, 93, 98]

>>> kthItem found median at index 10 with value of 55

passes

TRIAL #3

The original array is:

[76, 20, 94, 16, 92, 93, 4, 15, 62, 8, 63, 95, 50, 21, 48, 58, 7, 53, 63, 27, 47]

The original array sorted would be:

[4, 7, 8, 15, 16, 20, 21, 27, 47, 48, 50, 53, 58, 62, 63, 63, 76, 92, 93, 94, 95]

>>> kthItem found median at index 10 with value of 50

passes

E pivot pivot e pivot Smaller Larger E pivot pivot e pivot Smaller Larger