Each edge is annotated with the current flow (initially zero) and the edge’s capacity. In general, a flow of x along an edge with capacity y is shown as x/y. 

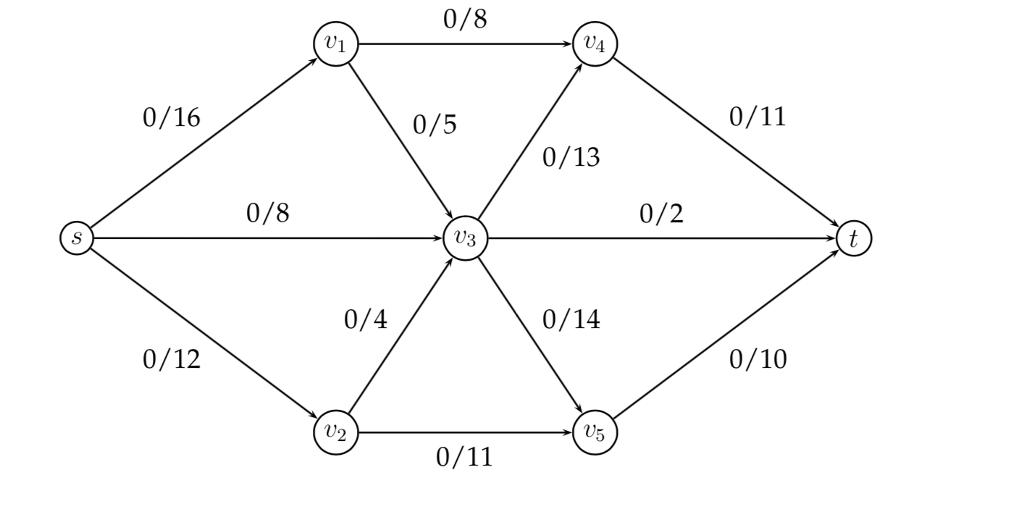
We will look at how the Ford-Fulkerson Algorithm operates on the following network.

a) Show the residual graph that will be created from this network with the given (empty) flow. In drawing a residual graph, to show a forward edge with capacity x and a backward edge with capacity y, annotate the original edge −→x ; ←−y . 

b) What is the bottleneck edge of the path (s, v1 , v3 , v5 , t) in the residual graph you have given in answer to Question 3a? 

c) Show the network with the flow that results from augmenting the flow based on the path (s, v1, v3, v5, t) of the residual graph you have given in answer to Question 3a. 

d) Show the residual graph for the network flow given in answer to Question 3c. 

e) What is the bottleneck edge of the path (s,v3,v4,t) in the residual graph you have given in answer to Question 3d?

f)  Show the network with the flow that results from augmenting the

flow based on the path (s, v3, v4, t) of the residual graph you have given in answer to Question 3d.

g)  Show the residual graph for the network flow given in answer to Question 3f.

h)  What is the bottle neck edge of the path(s,v2,v3,v1,v4,t)in the residual graph you have given in answer to Question 3g?

i)  Show the network with the flow that results from augmenting the flow based on the path (s,v2,v3,v1,v4,t) of the residual graph you have given in answer to Question 3g.

j)  Show the residual graph for the network flow given in answer to Question 3i.

k)  Show the final flow that the Ford-Fulkerson Algorithm finds for this network, given that it proceeds to completion from the flow rates you have given in answer to Question 3i, and augments flow along the edges (s, v1, v3, t) and (s, v2, v5, t).

l)  Identify acut of the network that has acut capacity equal to the maximum flow of the network. 

0/8 V1 V 0/11 0/16 0/5 0/13 0/8 0/2 V3 0/4 0/14 0/10 0/12 V2 U5 0/11