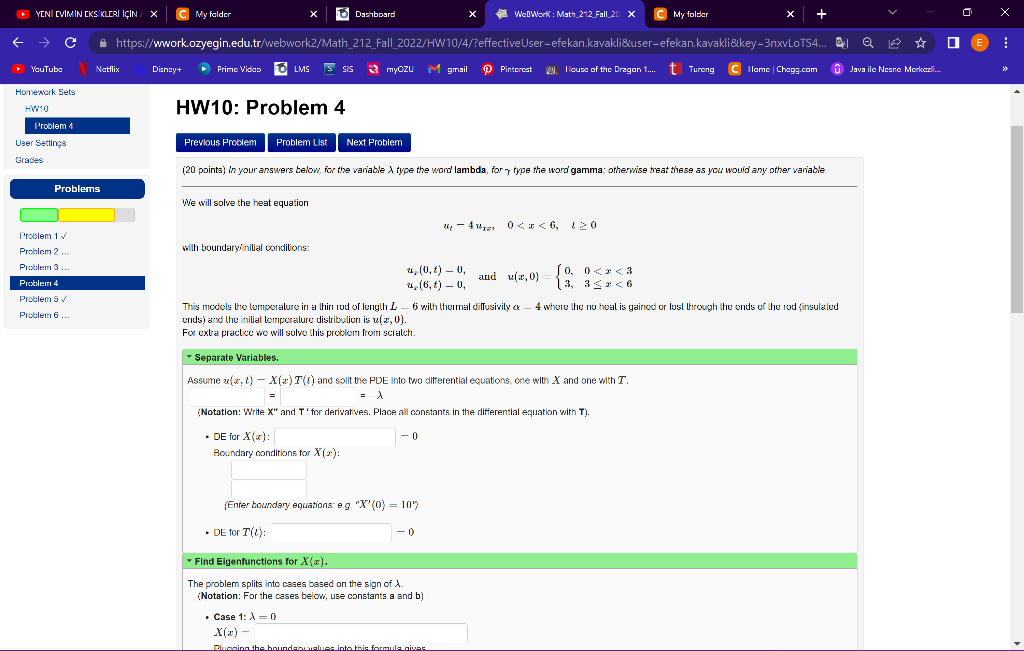
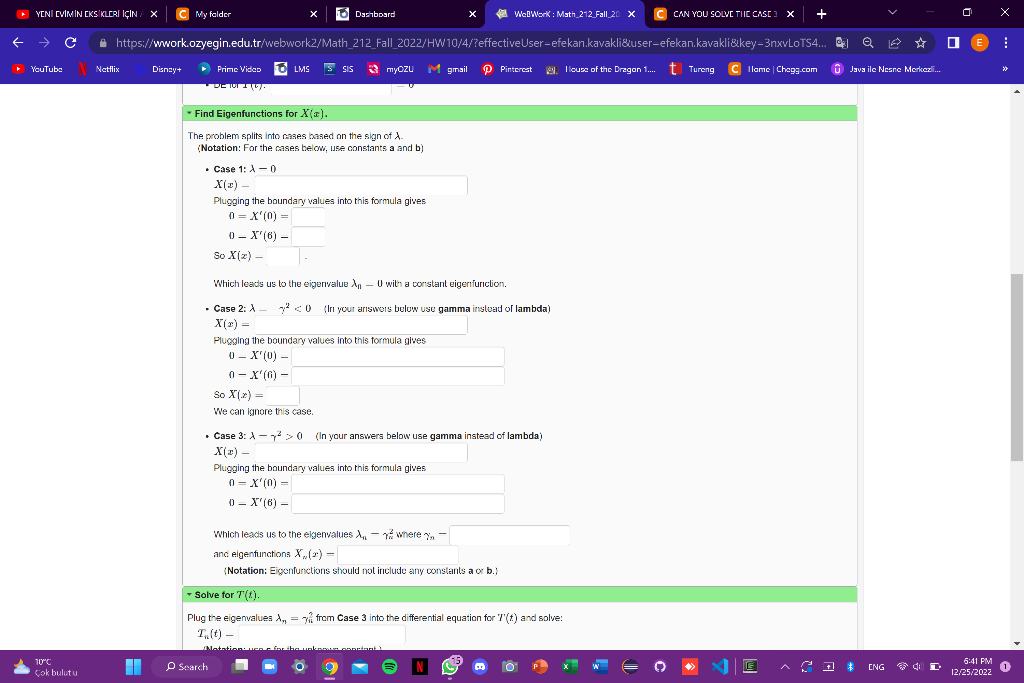
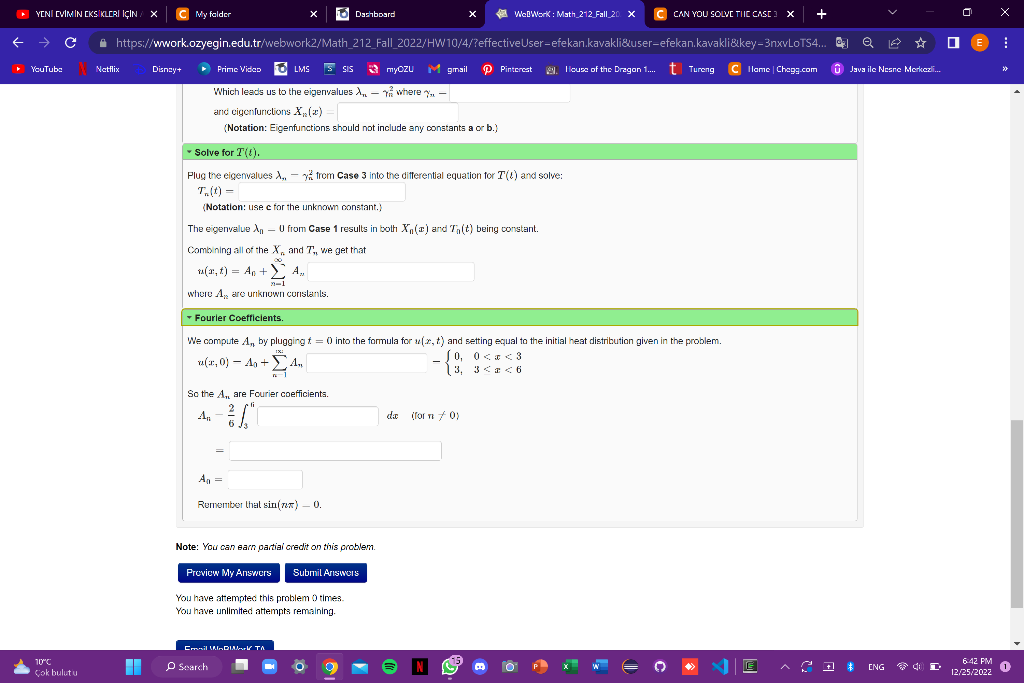
We will solve the heat equation ut4ux10x6,&00 with boundaryinitial ponditions: ui(0,t)0,u2(6,t)0,andu(x,0)={0,3,00 (In your answers below use gamma instead of lambdaj X(x) Plugging me Dounoary values nro rns tormula gives 0=X(0)=0X(6)= Which leacs us to the elgenvalues nn2 where n and eigenfunctions Xu(x)= (Notation: Eigenfunctions should not include any constants a orb.) Solve for T(t) Plug the eigenvalues n=in2 from Case 3 into the differential equation for ' T ( t ) and solve: Which leads us to the eigenvalues nn2 where n anc cigcnfunctions Xn(x) (Notation: Eigenfunctions should not include any constants a or b.) - Solve for T(t). Plug the eigenvalues nn2 from Case 3 into the differential equation for T(t) and solve: Tn(t)= (Notation: use c for the unknown constant.) The ecenvalue n0 from Case 1 results in both Xn(x) and Tn(t) being constant. Combining all of the Xn and Tn we get that u(a,t)=An+n=1An where A. are uriknown corislanks. - Fourier Coefficients. We compute An by plugging t=0 into the formula for u(x,t) and setting equal to the initial So the An are Fourier coefficients. AnAn623rdiiforn=0== Remember that sin(n)0. Note: You can earn partiai credit on this problem. You have atempted this problem 0 times. You have unlimited attempts remaining. We will solve the heat equation ut4ux10x6,&00 with boundaryinitial ponditions: ui(0,t)0,u2(6,t)0,andu(x,0)={0,3,00 (In your answers below use gamma instead of lambdaj X(x) Plugging me Dounoary values nro rns tormula gives 0=X(0)=0X(6)= Which leacs us to the elgenvalues nn2 where n and eigenfunctions Xu(x)= (Notation: Eigenfunctions should not include any constants a orb.) Solve for T(t) Plug the eigenvalues n=in2 from Case 3 into the differential equation for ' T ( t ) and solve: Which leads us to the eigenvalues nn2 where n anc cigcnfunctions Xn(x) (Notation: Eigenfunctions should not include any constants a or b.) - Solve for T(t). Plug the eigenvalues nn2 from Case 3 into the differential equation for T(t) and solve: Tn(t)= (Notation: use c for the unknown constant.) The ecenvalue n0 from Case 1 results in both Xn(x) and Tn(t) being constant. Combining all of the Xn and Tn we get that u(a,t)=An+n=1An where A. are uriknown corislanks. - Fourier Coefficients. We compute An by plugging t=0 into the formula for u(x,t) and setting equal to the initial So the An are Fourier coefficients. AnAn623rdiiforn=0== Remember that sin(n)0. Note: You can earn partiai credit on this problem. You have atempted this problem 0 times. You have unlimited attempts remaining