What is less probable: 1) to get 80 or more tails out of tossing a fair coin 100

times, 2) to get 30 or more tails out of tossing a fair coin 50 times. NOTE:

Since n > 30 you can assume that the cumulative distribution of the mean

is approximately Gaussian.

4. An experimenter inserts intracellular electrodes on a large sample of randomly selected neurons in primary visual cortex (V1). Intracellular electrodes are designed to measure the response of single neurons. The researcher finds the average response of the neurons is 10 mVolts and the

standard deviation 1 mVolt. On a subsequent experiment the researcher

inserts extracellular electrodes on randomly selected location in V1. Extracellular electrodes compute the average response of a number of neurons

around the tip of the electrode. The researcher finds that when the electrode

is extracellular the average response is still 10 mVolts but the standard deviation goes down to 0.01 mVolts. Assume the neurons in V1 are independent

and have identical response distributions.

(a) Explain how the standard deviation of the mean of n independent random variables changes as the number of random variables increases.

(b) Estimate how many neurons are having an effect on the extracellular

electrode. Justify your response

8. You know the minimum, the maximum, and the 25th, 50th, and 75th percentiles

of a distribution. Which of the following measures of central tendency or

variability can you determine?

mean, median, mode, trimean, geometric mean, range, interquartile range,

variance, standard deviation

9. For the numbers 1, 3, 4, 6, and 12:

Find the value (v) for which ?(X-v)2 is minimized.

Find the value (v) for which ?|x-v| is minimized.

10. Your younger brother comes home one day after taking a science test. He says

that some- one at school told him that "60% of the students in the class scored

above the median test grade." What is wrong with this statement? What if he had

said "60% of the students scored below the mean?

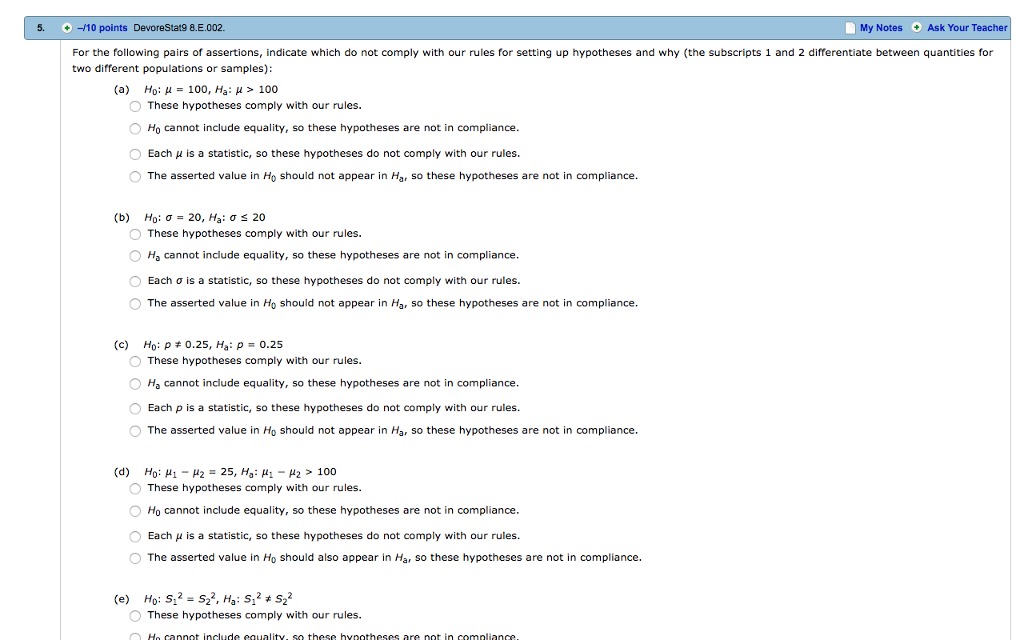
1. [12 mark(s)] Nathan is on trial for a murder, Based on all the evidence presented in court so far, the jury knows that the murderer was a man, and has narrowed things down to the following four mutually exclusive hypotheses with their corresponding prior probabilities: Hypothesis Definition Prior Probability N Nathan did it 0.5 Nathan's brother Mike did it 0.2 Nathan's friend John did it 0.2 Someone else did it 0.1 Suppose that Nathan and Mike always wear size ten shoes, John wears size ten shoes about half of the time, and in general about 25% of men wear size ten shoes. (b) [3 mark(s)] The murderer's shoeprint is found at the scene, and it is of a size ten shoe. Let D for data be the statement that the murderer wore size ten shoes. Assign likelihood values for the four hypotheses. You can assume that the proportions given in the question can be directly translated into probabilities. (e) [3 mark(s)] Calculate the posterior probabilities using a Bayes Box. (d) [2 mark(s)] Write down Bayes' rule in a form that is equivalent to one row of your Bayes Box. (e) [3 mark(s)) Write down the expression for the marginal likelihood in terms of the statements involved in this question, and give an interpretation of this quantity.5. -/10 points DevoreStat9 8.E.002. My Notes @ Ask Your Teacher For the following pairs of assertions, indicate which do not comply with our rules for setting up hypotheses and why (the subscripts 1 and 2 differentiate between quantities for two different populations or samples): (a) Ho: M = 100, Ha: H > 100 O These hypotheses comply with our rules. Ho cannot include equality, so these hypotheses are not in compliance. Each u is a statistic, so these hypotheses do not comply with our rules. ) The asserted value in Ho should not appear in Ha, so these hypotheses are not in compliance. (b) Ho: G = 20, Ha: 0 = 20 O These hypotheses comply with our rules. O Ha cannot include equality, so these hypotheses are not in compliance. Each o is a statistic, so these hypotheses do not comply with our rules. O The asserted value in Ho should not appear in Ha, so these hypotheses are not in compliance. (c) Ho: p # 0.25, Ha: p = 0.25 These hypotheses comply with our rules. O He cannot include equality, so these hypotheses are not in compliance. O Each p is a statistic, so these hypotheses do not comply with our rules. O The asserted value in Ho should not appear in Ha, so these hypotheses are not in compliance. (d) Ho: 1 - H2 = 25, Ha: #1 - #2 > 100 These hypotheses comply with our rules. O Ho cannot include equality, so these hypotheses are not in compliance. Each # is a statistic, so these hypotheses do not comply with our rules. The asserted value in Ho should also appear in Ha, so these hypotheses are not in compliance. (e) Ho: 512 = 527, Ha: 512 # 522 O These hypotheses comply with our rules.1. Use Naive Bayes classification method (and the Bayes classification rule) to classify the following two feature vectors: a. [X/ = 1, X2 = 1, X3 = 0] b. [X1 = 0, X2 = 1, X3 = 0] Table 1 gives the training data to estimate probabilities. The class labels are 0 or 1. Use 3 as the m-value i.e. m = 3 and use prior probability as 0.5 i.e., p = 0.5 Table 1. Labeled training data. XI X2 X3 Class Label 0 0 0 0 0 U O 0 Page 1 of 2 2. Use Tree Augmented Naive Bayes (and the Bayes classification rule) to classify the two feature vectors. (Don't use m-estimate for the probabilities.)2. A scientist is considering three different hypotheses: Hi. H2, and H3. Before observing any new evidence, she has the following degrees of belief: Pr(H1) = 0.1 Pr(E | H1) = 0.5 Pr(H2) = 0.2 Pr(E | H2) = 0 Pr(H3) = 0.7 Pr(E | H3) = 0.4 Given her initial degrees of belief, according to Bayes' rule, if she observes that E is the case, she should update her initial degrees of belief in her hypotheses to the following: Pr(H1) = 0.15 Pr(H2) = 0 Pr(H3) = 0.85