what is the analyis and algorithm in steps for "Analysis of QuickSort Pivots"

worst-case performance of QuickSort can be either O(n^2) or O(n log n), depending on how you choose the pivot. The purpose of this assignment is to investigate this more deeply.

Starting with our QuickSort implementation from Blackboard (not any other implementation), measure its performance on random arrays and arrays that are already sorted in either ascending or descending order.

Then, modify our QuickSort implementation from Blackboard to choose the pivot more carefully. (Refer to Slide 30 of the lecture notes.) Note that in several parts of the quickSortStep() code, starting from line 4 of that function, it assumes that the pivot is in the right-most array position. Therefore, one easy way to modify the implementation is: (1) pick a different pivot location; (2) swap the element at that location with the rightmost array element, to move your pivot to the rightmost position. Then you wont need to change subsequent lines.

Again, test your modified implementation on both random arrays and sorted (ascending/descending) arrays. Present your results with a table and plot.

/** QuickSort.java: * * Based on code from Goodrich & Tamassia, Data Structures and Algorithms in Java * With some simplifications for clarity, and test code at the end. */ import javax.swing.JOptionPane; import java.util.Comparator; public class QuickSort { /** QuickSort method: * Sorts the elements of array arr in nondecreasing order according * to comparator c, using the quick-sort algorithm. Most of the work * is done by the auxiliary recursive method quickSortStep. **/ public static void quickSort (Object[] arr, Comparator c) { if (arr.length = rightBound) return; // the indices have crossed Object temp; // temp object used for swapping // Set the pivot to be the last element Object pivotValue = s[rightBound]; // Now partition the array int upIndex = leftBound; // will scan rightward, 'up' the array int downIndex = rightBound-1; // will scan leftward, 'down' the array while (upIndex = upIndex) && (c.compare(s[downIndex], pivotValue)>=0)) downIndex--; if (upIndex  
(last assignment was Sorting Algorithm Analysis given below)
 
import java.util.Comparator;
 
public class Analysis {
 
 private static int moves = 0; private static int compares = 0;
 
 public static void main(String[] args){ String arr[] = {"a", "hello", "x", "w", "q", "h", "d", "p", "a1", "x2", "w2", "q1", "2h", "2d", "3p", "1a", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "g3x", "g2w", "f3q", "fh4", "gd4", "f4p", "f3a", "d3x", "s5w", "sq5", "sh5", "dd5", "sp5"};
 
 //String arr2[] = (String[])arr.clone(); //String arr3[] = (String[])arr.clone(); //quickSort(arr, new StringComparator()); //insertionSort(arr2); //shellSort(arr3); //System.out.println("Quick Sort -------------- Num Comparisons: " + quickCompare + " Num Moves: " + quickMove + " "); //insertionSort(arr2); //System.out.println("Insertion Sort -------------- Num Comparisons: " + insertCompare + " Num Moves: " + insertMove + " "); //insertMove = 0; //insertCompare = 0; //shellSort(arr3); //System.out.println("Shell Sort -------------- Num Comparisons: " + insertCompare + " Num Moves: " + insertMove + " "); //String[] rand = randomStringArray(10); //System.out.println(array2String(rand)); Performance(5000); Performance(10000); Performance(25000); //Performance(50000); //Performance(100000);
 
 }
 
 private static void insertionSort(Comparable[] a, int first, int last, int gap) { int index; // general index for keeping track of a position in array int toSort; // stores the index of an out-of-place element when sorting.
 
 for (toSort = first+gap; toSort  
 boolean moveMade = false; index = toSort - gap; while ((index >= first) && (toSortElement.compareTo(a[index])  
 public static void insertionSort(Comparable arr[]) { insertionSort(arr, 0, arr.length-1, 1); }
 
 public static void shellSort (Comparable[] arr) { int last = arr.length-1;
 
 // Begin with gap = half length of array; reduce by half each time. for (int gap = arr.length/2; gap > 0; gap = gap/2) { if (gap % 2 == 0) gap++; // if gap is even, move to next largest odd number
 
 // Apply Insertion Sort to the subarrays defined by the gap distance for (int first = 0; first  
 //QuickSort method:
 
 public static void quickSort (Object[] arr, Comparator c) { if (arr.length  
 //QuickSortStep method:
 
 private static void quickSortStep (Object[] s, Comparator c, int leftBound, int rightBound ) { if (leftBound >= rightBound){ return; // the indices have crossed } Object temp; // temp object used for swapping
 
 // Set the pivot to be the last element Object pivotValue = s[rightBound];
 
 // Now partition the array int upIndex = leftBound; // will scan rightward, 'up' the array int downIndex = rightBound-1; // will scan leftward, 'down' the array while (upIndex  
 // scan leftward to find an element smaller than the pivot while ( (downIndex >= upIndex) && (c.compare(s[downIndex], pivotValue)>=0)){ downIndex--; compares++; }
 
 if (upIndex  
 int pivotIndex = upIndex; temp = s[rightBound]; // swap pivot with the element at upIndex s[rightBound] = s[pivotIndex]; s[pivotIndex] = temp; moves += 3;
 
 // the pivot is now at upIndex, so recursively quicksort each side quickSortStep(s, c, leftBound, pivotIndex-1); quickSortStep(s, c, pivotIndex+1, rightBound); }
 
 /** utility method to return string representation of array of strings */ private static String array2String(String[] a) { String text="["; for (int i=0; i 
 private static String[] randomStringArray(int size){ String[] a = new String[size]; for(int i = 0; i  
 //Performs 3 Trials for Each Sorting Algorithm and Averages the Results public static void Performance(int size){ long shellMoves = 0; long shellCompares = 0; long quickMoves = 0; long quickCompares = 0; long insertMoves = 0; long insertCompares = 0;
 
 String[] shell1 = randomStringArray(size); String[] shell2 = (String[])shell1.clone(); String[] shell3 = (String[])shell1.clone();
 
 String[] quick1 = (String[])shell1.clone(); String[] quick2 = (String[])shell1.clone(); String[] quick3 = (String[])shell1.clone();
 
 String[] insert1 = (String[])shell1.clone(); String[] insert2 = (String[])shell1.clone(); String[] insert3 = (String[])shell1.clone();
 
 long startTime = System.currentTimeMillis(); shellSort(shell1); long endTime = System.currentTimeMillis(); long shellTrial1Time = endTime - startTime; shellMoves += moves; shellCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); shellSort(shell2); endTime = System.currentTimeMillis(); long shellTrial2Time = endTime - startTime; shellMoves += moves; shellCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); shellSort(shell3); endTime = System.currentTimeMillis(); long shellTrial3Time = endTime - startTime; shellMoves += moves; shellCompares += compares; moves = 0; compares = 0; shellMoves /= 3; shellCompares /= 3;
 
 startTime = System.currentTimeMillis(); quickSort(quick1, new StringComparator()); endTime = System.currentTimeMillis(); long quickTrial1Time = endTime - startTime; quickMoves += moves; quickCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); quickSort(quick2, new StringComparator()); endTime = System.currentTimeMillis(); long quickTrial2Time = endTime - startTime; quickMoves += moves; quickCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); quickSort(quick3, new StringComparator()); endTime = System.currentTimeMillis(); long quickTrial3Time = endTime - startTime; quickMoves += moves; quickCompares += compares; moves = 0; compares = 0; quickMoves /= 3; quickCompares /= 3;
 
 startTime = System.currentTimeMillis(); insertionSort(insert1); endTime = System.currentTimeMillis(); long insertionTrial1Time = endTime - startTime; insertMoves += moves; insertCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); insertionSort(insert2); endTime = System.currentTimeMillis(); long insertionTrial2Time = endTime - startTime; insertMoves += moves; insertCompares += compares; moves = 0; compares = 0;
 
 startTime = System.currentTimeMillis(); insertionSort(insert3); endTime = System.currentTimeMillis(); long insertionTrial3Time = endTime - startTime; insertMoves += moves; insertCompares += compares; moves = 0; compares = 0; insertMoves /= 3; insertCompares /= 3;
 
 long averageShellTime = (shellTrial1Time + shellTrial2Time + shellTrial3Time) / (3); long averageQuickTime = (quickTrial1Time+ quickTrial2Time + quickTrial3Time) / (3); long averageInsertionTime = (insertionTrial1Time+ insertionTrial2Time + insertionTrial3Time) / (3);
 
 System.out.println("Average Sorting Algorithm Perfomance for a String Array of size " + size + " Over 3 Trials ===================="); System.out.println("Quick Sort -------------- Num Comparisons: " + quickCompares + " Num Moves: " + quickMoves + " Time: " + averageQuickTime + "ms "); System.out.println("Insertion Sort -------------- Num Comparisons: " + insertCompares + " Num Moves: " + insertMoves + " Time: " + averageInsertionTime+ "ms "); System.out.println("Shell Sort -------------- Num Comparisons: " + shellCompares + " Num Moves: " + shellMoves + " Time: " + averageShellTime + "ms ");
 
 }
 
 } ------------------------------------------------------------------- import javax.swing.JOptionPane;
 
public class InsertSort { private static void insertionSort(Comparable[] a) { int index; // general index for keeping track of a position in array int toSort; // stores the index of an out-of-place element when sorting. int last = a.length-1;
 
 for (toSort = 1; toSort  
 boolean moveMade = false; // Minor optimisation, also used in messages displayed index = toSort - 1; while ((index >= 0) && (toSortElement.compareTo(a[index])  
 /** Main method to test insertionSort */ public static void main(String[] args) { String arr[] = {"W","B","Z","Q","M"}; //Integer arr[] = {12, 17, 3, 2000, 2001, 99, 203};
 
 /* String arr[] = {"a", "hello", "x", "w", "q", "h", "d", "p", "a1", "x2", "w2", "q1", "2h", "2d", "3p", "1a", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "q3x", "q2w", "3qq", "qh4", "ad4", "4ap", "3aa", "3ax", "a5w", "q5", "fh5", "fd5", "fp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "n3x", "2bw", "n3q", "nh4", "nd4", "n4p", "b3a", "b3x", "c5w", "xq5", "kh5", "dj5", "jp5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "3x", "2w", "3q", "h4", "d4", "4p", "3a", "3x", "5w", "q5", "h5", "d5", "p5", "g3x", "g2w", "f3q", "fh4", "gd4", "f4p", "f3a", "d3x", "s5w", "sq5", "sh5", "dd5", "sp5"}; */
 
 JOptionPane.showMessageDialog(null, "Array length is "+ arr.length); JOptionPane.showMessageDialog(null, "Array before sorting: " + array2String(arr)); insertionSort(arr); JOptionPane.showMessageDialog(null, "Array after sorting with Insertion Sort: " + array2String(arr));
 
 System.exit(0); }
 
 /** Utility method to return string representation of array of strings */ private static String array2String(Object[] a) { String text="["; for (int i=0; i 
 } --------------------------------------------------------------- import javax.swing.JOptionPane;
 
public class ShellSort { //Sorts equally spaced elements of an array into ascending order.
 
 public static void shellSort (Comparable[] arr) { int last = arr.length-1;
 
 // Begin with gap = half length of array; reduce by half each time. for (int gap = arr.length/2; gap > 0; gap = gap/2) { if (gap % 2 == 0) gap++; // if gap is even, move to next largest odd number
 
 // Apply Insertion Sort to the subarrays defined by the gap distance for (int first = 0; first  
 private static void insertionSort(Comparable[] a, int first, int last, int gap) { int index; // general index for keeping track of a position in array int toSort; // stores the index of an out-of-place element when sorting.
 
 for (toSort = first+gap; toSort  
 boolean moveMade = false; index = toSort - gap; while ((index >= first) && (toSortElement.compareTo(a[index])  
 public static void insertionSort(Comparable arr[]) { insertionSort(arr, 0, arr.length-1, 1); }
 
 /** M Madden: Main method to test shellSort */ public static void main(String[] args) { String[] arr = {"aa", "xa", "bq", "aq", "sw2", "ph", "pp"};
 
 // we can also use insertionSort directly String copy2[] = arr.clone();
 
 JOptionPane.showMessageDialog(null, "Array length is "+ copy2.length);
 
 JOptionPane.showMessageDialog(null, "Array before sorting with InsertionSort " + array2String(copy2));
 
 insertionSort(copy2); JOptionPane.showMessageDialog(null, "After Sorting with InsertionSort: " + array2String(copy2));
 
 String copy[] = arr.clone();
 
 JOptionPane.showMessageDialog(null, "Array before sorting with Shell Sort: " + array2String(copy));
 
 shellSort(copy); JOptionPane.showMessageDialog(null, "After Shell Sort" + array2String(copy));
 
 System.exit(0); }
 
 /** M Madden: utility method to return string representation of array of strings */ private static String array2String(String[] a) { String text="["; for (int i=0; i 
 } ----------------------------------------------- import javax.swing.JOptionPane; import java.util.Comparator;
 
 public class QuickSort { public static void quickSort (Object[] arr, Comparator c) { if (arr.length  
 private static void quickSortStep (Object[] s, Comparator c, int leftBound, int rightBound ) { if (leftBound >= rightBound) return; // the indices have crossed Object temp; // temp object used for swapping
 
 // Set the pivot to be the last element Object pivotValue = s[rightBound];
 
 // Now partition the array int upIndex = leftBound; // will scan rightward, 'up' the array int downIndex = rightBound-1; // will scan leftward, 'down' the array while (upIndex = upIndex) && (c.compare(s[downIndex], pivotValue)>=0)) downIndex--; if (upIndex  
 int pivotIndex = upIndex; temp = s[rightBound]; // swap pivot with the element at upIndex s[rightBound] = s[pivotIndex]; s[pivotIndex] = temp;
 
 // the pivot is now at upIndex, so recursively quicksort each side quickSortStep(s, c, leftBound, pivotIndex-1); quickSortStep(s, c, pivotIndex+1, rightBound); }
 
 /** Main method to test QuickSort */ public static void main(String[] args) { //String arr[] = {"5", "3", "2", "6"}; String arr[] = {"This", "is","yet", "another", "Boring", "Array", "Sorting", "test"}; JOptionPane.showMessageDialog(null, "Array before sorting: " + array2String(arr));
 
 // quickSort method's first parameter is just the array; quickSort(arr, new StringComparator());
 
 JOptionPane.showMessageDialog(null, "Array after sorting: " + array2String(arr)); }
 
 /** utility method to return string representation of array of strings */ private static String array2String(String[] a) { String text="["; for (int i=0; i 
/** Comparator class for case-insensitive comaprison of strings */ class StringComparator implements Comparator { public int compare(Object ob1, Object ob2) { String s1 = (String)ob1; String s2 = (String)ob2; //return s1.compareTo(s2); // use compareTo for case-sensitive comparison return s1.compareToIgnoreCase(s2); } }
 
 
 
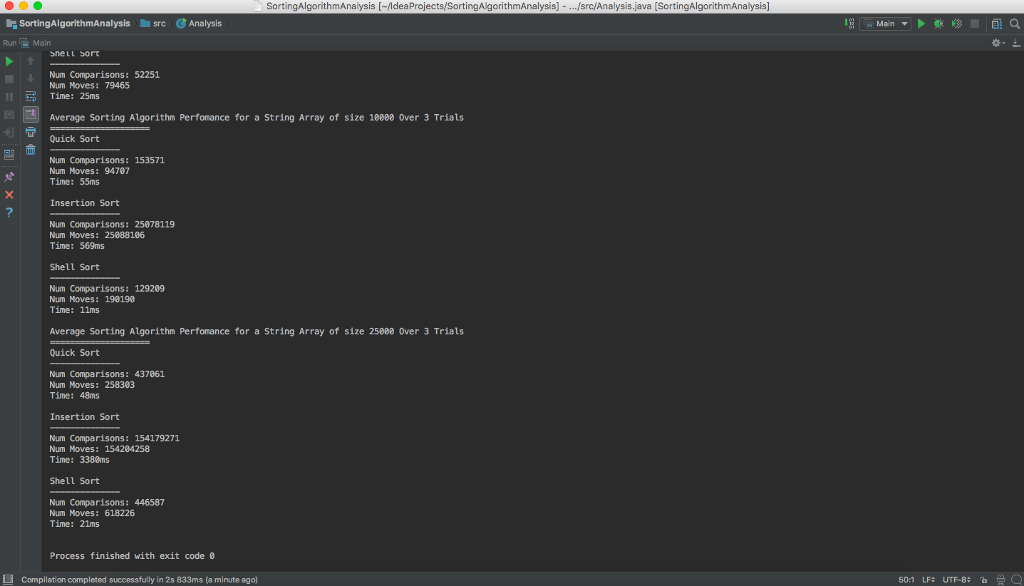
  SortingAlgorithmAnalysisldeaProjects/SortingAlgorithmAnalysis] - .srcAnalysis.java [SortingAlgorithmAnalysis] SortingAlg src Analysis Run Main Num Comparisons: 52251 Num Mowes: 79465 Time: 25ms Average Sorting Algorithm Perfomance for a String Array of size 18880 Over 3 Trials Quick Sort ? Num Comparisons: 153571 Num Moves: 94707 Time: 55ms Insertion Sort Num Comparisons: 25078119 Num Moves: 25888186 Time: 569ms Shell Sort Num Comparisons: 129209 Num Mowes: 190190 Time: 11ms Average Sorting Algorithm Perfomance for a String Array of size 25880 Over 3 Trials Quick Sort Num Comparisons: 437061 Num Moves: 258303 Time: 48ms Insertion Sort Num Comparisons: 154179271 Num Moves: 154204258 Time: 3380ms Shell Sort Num Comparisons: 446587 Num Moves: 618226 Time: 21ms Process finished with exit code 0 Compilation completed successfully in 2s 833ms (a minute ago] 50:1 LF# UTF-8