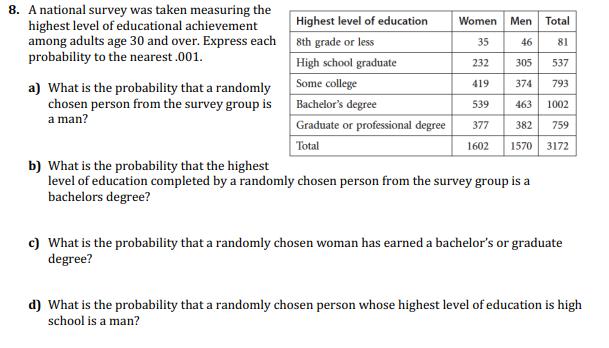
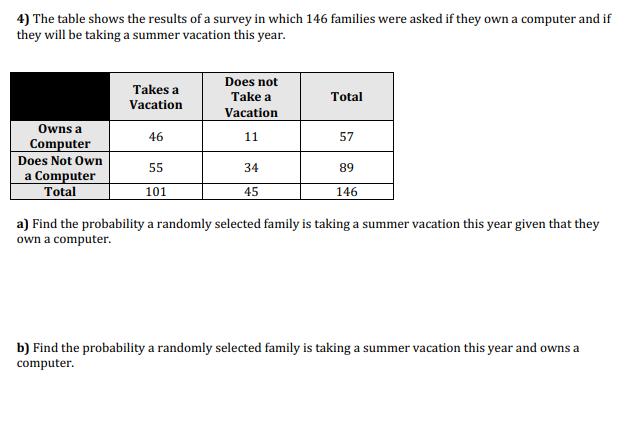
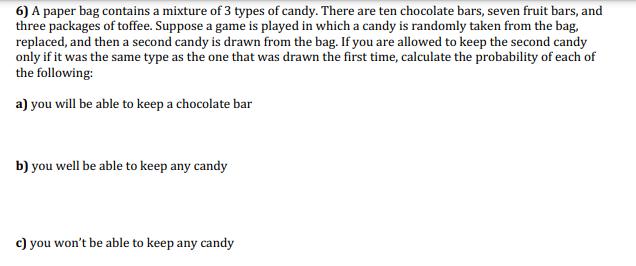
What is the probability of choosing a King from a standard deck of 52 playing cards? What is the probability of choosing a green marble from a jar containing 5 red, 6 green and 4 blue marbles? What is the probability of choosing a marble that is not blue in problem 2? What is the probability of getting an odd number when rolling a single 6-sided die? What is the probability of choosing a jack or a queen from a standard deck of 52 cards? What is the probability of landing on an odd number after spinning a spinner with 7 equal sectors numbered 1 through 7? What is the probability of choosing a queen, a king or an ace from a standard deck of playing cards? 8. A national survey was taken measuring the highest level of educational achievement among adults age 30 and over. Express each probability to the nearest .001. a) What is the probability that a randomly chosen person from the survey group is a man? Highest level of education 8th grade or less High school graduate Some college Bachelor's degree Graduate or professional degree Total Women Men Total 35 46 81 232 305 537 419 374 793 539 463 1002 377 382 759 1602 1570 3172 b) What is the probability that the highest level of education completed by a randomly chosen person from the survey group is a bachelors degree? c) What is the probability that a randomly chosen woman has earned a bachelor's or graduate degree? d) What is the probability that a randomly chosen person whose highest level of education is high school is a man? Jagged Array Introduction A jagged array is an array of arrays of which the member arrays can be of different lengths, producing rows of jagged edges when visualized as output. In contrast, two-dimensional arrays are always rectangular, so jagged arrays should not be confused with multidimensional arrays. A jagged array is useful when you have data in two dimensions that may not be fully matrixed. When 2D arrays become very large, entries with lots of Os become very wasteful in terms of space. Representations There are two possible representations of jagged arrays. The default representation is the unpacked one. In this representation (shown on the left in the figure below), the array actually looks jagged. The unpackedValues member holds a bin of objects stored at that array index. This example has seven bins holding six elements. Your Task Your task is to implement the JaggedArray class in JaggedArray.java. A skeleton is already given to you. Your implementation must use the member variables unpackedValues, packedValues and offsets. Your representation should use java.util.Linked List. This is a Java class representing a linked list that you can use without having to write your own. These member variables are declared private, as they should be. However, the testing code uses public accessors to look at the values of your representation, so don't change those accessors. You have to implement these methods: public JaggedArray (int bins) -- Create a jagged array with the given number of bins. public int size() -- Return the number of elements stored in the jagged array public int numberOfBins () -- Return the number of bins in the jagged array public int numberOfSlots (int bin) Return the number of slots stored in the given bin. This needs to work for both packed and unpacked representations. public T get Element(int bin, int slot) -- Return the element stored at the given bin and slot number. Throw an IndexOutOfBounds Exception if the bin or slot is invalid. This needs to work for both packed and unpacked representations. public boolean addElement(int bin, T element) - Add the element to the given bin. Return true if successful, or false if the representation is packed. Throw an IndexOutOfBounds Exception if the bin is invalid. -- public boolean removeElement(int bin, int slot) - Remove the element from the given bin and slot. Return true if successful, or false if the representation is packed. Throw an IndexOutOfBounds Exception if the bin or slot is invalid. public boolean unpack() - Unpack the jagged array. Return true if successful, or false if the array is already unpacked. public boolean pack() - Pack the jagged array. Return true if successful, or false if the array is already packed. Testing and Debugging The JaggedArray class has a member function called "print" that prints out the jagged array. It should help you in debugging your code. I suggest writing a main function and exercising your code with a few add and remove, pack and unpack operations, then printing out the array and seeing if it's what you expect. The test code is in the Test directory in TestJagged Array.java. To test your code, type: make test Java Generics The Jagged Array class uses Java generics to hold elements of generic type T. In order to create a JaggedArray that holds characters, we invoke it with: JaggedArray jagged = new JaggedArray (10); This creates a jagged array with Character elements and ten bins. Java generics can be tricky to use. This link is useful to study when you're trying to create an array of LinkedLists in Java. 9. Two fair dice are rolled. a) What is the probability that the second die lands on a higher value than does the first? b) What is the probability that the sum of the values is a prime number? FIRST ROLL d) What is the probability that the sum of the dice is 9? T 2 3 4 SECOND ROLL 1 (1.1) (2.1) (3,1) (5.1) 5 (1.2) (1.3) (14) (1.5) (1.6) 3 (3.2) (3.3) (34) (3,5) (36) (5.50 63) (54) 6.5) 6.6) (6.2) (6.5) (6,4) (6.5) (5,6) c) What is the probability the sum of the digits is a prime assuming the first dice rolled a value of either 3 or a 4. HAFH ("Home Away from Home") Realty Company leases apartments to corporate clients, HAFH Realty Company Property Management Database will keep track of HAFH buildings, apartments, corporate clients, building managers, cleaning staff members, and building inspectors. The property management database for the realty company HAFH will capture data about the following: For each building: BuildingID (unique) and BNoOfFloors (number of floors in the building); For each apartment: AptNo (partially unique, i.e., unique within a building) and ANOOf Bedrooms (number of bedrooms in the apartment); For each corporate client: CCID (unique), CCName (unique), CCLocation, and CCIndustry; For each manager: ManagerID (unique), MFullName (composed of MFirstName and MLastName), multiple MPhone numbers, MBDate, Mage (derived from MBdate and current date), MSalary, and MBonus (not every manager will have a bonus); For each staff member: SMemberID (unique) and SMemberName; For each inspector: InsID (unique) and InsName; Each building has one or more apartments. Each apartment is located in exactly one building. Each apartment is either leased to one corporate client or to no one. Each corporate client leases between zero and many apartments. Each corporate client refers between zero and many corporate clients. Each corporate client can be referred by one corporate client or is not referred by any. Each apartment is cleaned by either one or two staff members. Each staff member cleans between five and ten apartments. Each manager manages one or many buildings. Each building is managed by exactly one manager. Each manager resides in exactly one building. Each building either has one manager residing in it or no managers residing in it. Each inspector inspects one or many buildings. Each building is inspected by one or many inspectors. For each building that a particular inspector inspects, the dates of the last inspection by the inspector and of the next future inspection by the inspector are recorded." BuildingID (BNoOfFloors) ManagerID) ResidesIn MPhone DateNext MAge Inspects BUILDING Manages MANAGER MBdate INSPECTOR Datelast LocatedIn MSalary MBonus (0) (MFullName) InsID MLastName InsName AntNo MFirstName) (5,10) ANoOfBedrooms APARTMENT Cleans (1,2) STAFFMEMBER Leases (SMemberID) (SMemberName) CCID CCName CCIndustry CORPCLIENT Refers CCLocation 5) A bag contains 12 identically shaped blocks, 3 of which are red and the remainder are green. The bag is well-shaken and a single block is drawn. a) What is the probability that the block is red? b) What is the probability that the block is not red? 6) Each of the letters for the word 'MATHEMATICS' is printed on same-sized pieces of paper and placed in a hat. That hat is shaken and one piece of paper is drawn. a) What is the probability that the letters S is selected? b) What is the probability that the letter M is selected? c) What is the probability that a vowel is selected? 7) Many board games involve a roll of two-six sided dice to see how far you may move your pieces. a) Copy and complete the following table that shows the totals for all possible rolls of two dice. b) What is the probability of rolling a 7? Second Die 1 2 3 4 5 6 First Die 1 2 3 4 5 c) What is the probability of not rolling a 7? d) What is the probability of rolling doubles? 8) What is the probability that a randomly drawn integer between 1 and 40 is not a perfect square? 9) A picnic cooler contains different types of cola: 12 regular, 8 cherry, 10 diet, 6 diet cherry, 8 caffeine- free, and some caffeine-free diet. You pick a can of cola without looking at its type. There is a 44% chance that the drink selected is diet. How many caffeine-free diet colas are in the cooler? 1) Using the Venn diagram below, list the number of elements in each of the following sets. a) PnQ b) PUQ c) XnQ d) XUQ e) YnQ 1) PnQnX b) P(A) = 0.7, P(B) = 0.2, P(AUB) =?, P(ANB) = 0.15 5 c) P(A) = 0.3, P(B) =?, P(AUB) = 0.9, P(ANB) = 0 4 6 X 12 Q 10 2) For each of the following, find the indicated probability and state whether A and B are mutually exclusive. a) P(A) = 0.5, P(B) = 0.2, P(AUB)= 0.7, P (ANB) =? S 3) The probability that Kelly will make the volleyball team is and the probability that she will make the field hockey team is. If the probability that she makes both teams is what is the probability that she makes at least one of the teams? 4) An aquarium at a pet store contains 20 guppies (12 females and 8 males) and 36 tetras (14 females and 22 males). If the clerk randomly nets a fish, what is the probability that it is a female or a tetra? 5) Teri attends a fundraiser at which 15 T-shirts are being given away as door prizes. Door prize winners are randomly given a shirt from a stock of 2 black shirts, 4 blue shirts, and 9 white shirts. Teri really likes the black and blue shirts, but is not too keen on the white ones. Assuming that Teri wins the first door prize, what is the probability that she will get a shirt that she likes? 6) A card is randomly selected from a standard deck of cards. What is the probability that either a heart or a face card (jack, queen, or king) is selected? 7) An electronics manufacturer is testing a new product to see whether it requires a surge protector. The tests show that a voltage spike has a 0.2% probability of damaging the product's power supply, a 0.6% probability of damaging downstream components, and a 0.1% probability of damaging both. Determine the probability that a voltage spike will damage the product. 8) At the start of flu season, Dr. Anna Ahmeed examines 50 patients over two days. Of those 50 patients, 30 have a headache, 24 have a cold, and 12 have neither symptom. Some patients have both symptoms. a) Draw a Venn diagram and determine the number of patients that have both symptoms. b) Find the probability that a patient selected at random.... i) has just a headache ii) iii) has a headache or a cold does not have cold symptoms 9) a) Use the table to complete the following Venn Diagram: b) What is the probability that a student plays volleyball? c) What is the probability that a student plays basketball? Team Volleyball Basketball Swimming VB and BB VB and Swim BB and Swim All three d) What is the probability that a student plays basketball and volleyball? e) What is the probability that a student plays basketball or volleyball? # of Students 15 12 10 8 4 4 3 1) Joel surveyed his class and summarized responses to the question, "Do you like school?" Disliked Liked 12 5 10 3 22 8 Males Females Total Find each of the following probabilities: a) P(likes school student is male) No Opinion 2 1 3 b) P (student is female | student dislikes school) Total 19 14 33 2) A person is chosen at random from shoppers at a department store. If the person's probability of having blonde hair and glasses is and the probability of wearing glasses is determine the probability that a person has blonde hair given that they wear glasses. 3) From a medical study of 10 000 male patients, it was found that 2500 were smokers; 720 died from lung cancer and of these, 610 were smokers. Determine: a) P(dying from lung cancer | smoker) b) P(dying from lung cancer | non-smoker) 4) The table shows the results of a survey in which 146 families were asked if they own a computer and if they will be taking a summer vacation this year. Owns a Computer Does Not Own a Computer Total Takes a Vacation 46 55 101 Does not Take a Vacation 11 34 45 Total 57 89 146 a) Find the probability a randomly selected family is taking a summer vacation this year given that they own a computer. b) Find the probability a randomly selected family is taking a summer vacation this year and owns a computer. 1) A truck driver has a choice of routes as he travels among four cities. He can choose from four routes between Toronto and Oakville, two between Oakville and Hamilton, and three between Hamilton and Guelph. Find the total number of routes possible for the complete Toronto-Oakville-Hamilton-Guelph trips. 2) A test has four true/false questions. What is the probability that they will get all four correct by guessing? 3) A test has three multiple choice questions, each question has four possible answers. What is the probability that you get all three questions correct by guessing? 4) A standard deck of cards has had all the face cards (jacks, queens, and kings) removed so that only the ace through ten of each suit remain. A game is played in which a card is drawn from this deck and a six- sided die is rolled. For the purpose of this game, an ace is considered to have a value of 1. a) Determine the total number of possible outcome for this game. b) Find the probability of each of these events: i) an even card and an even roll of the die ii) an even card and a roll of 3. iii) a card of 3 and a roll of the die of 3 or less 5) Suppose the two joker cards are left in a standard deck of cards. One of the jokers is red and the other is black. A single card is drawn from the deck of 54 cards, returned, and then a second card is drawn. Determine the probability of drawing: a) one of the jokers on the first draw and an ace on the second b) the red joker on the second draw and a numbered card of any suit on the first c) a queen on both draws d) any black card on both draws e) any numbered card less than 10 on the first draw and a card with the same number on the second 6) A paper bag contains a mixture of 3 types of candy. There are ten chocolate bars, seven fruit bars, and three packages of toffee. Suppose a game is played in which a candy is randomly taken from the bag, replaced, and then a second candy is drawn from the bag. If you are allowed to keep the second candy only if it was the same type as the one that was drawn the first time, calculate the probability of each of the following: a) you will be able to keep a chocolate bar b) you well be able to keep any candy c) you won't be able to keep any candy 7) A coin is tossed and a standard six-sided die is rolled. a) How many different outcomes are possible? b) What is the probability of flipping tails and rolling a number greater than 4? 8) The probability that a salmon swims successfully through a dam is 0.85. a) Find the probability that three salmon swim successfully through the dam. b) Find the probability that none of the three salmon is successful. c) Find the probability that at least one of the three salmon is successful in swimming through the dam. 9) There are two tests for a particular antibody. Test A gives a correct result 95% of the time. Test B is accurate 89% of the time. If a patient is given both tests, find the probability that a) both tests give the correct result b) neither test gives the correct result c) at least one of the tests gives the correct result 1) Evaluate each of the following a) 5! b) SP3 c) d) P (10, 3) 2) Simplify each of the following n! (n-1)! 3) Express the following using factorials a) 5x4x3x2x1 b) (3n)! (3n-1)! b) 8x7x6 30x29x28 3x2x1 4) Ten students are to line up for a photograph. a) In how many ways can the 10 students standing in a line be arranged? b) In how many ways can the 10 students standing in a line be arranged if Jill must be first? c) In how many ways can 10 students standing in a line be arranged if Jill must be first and Meera last?