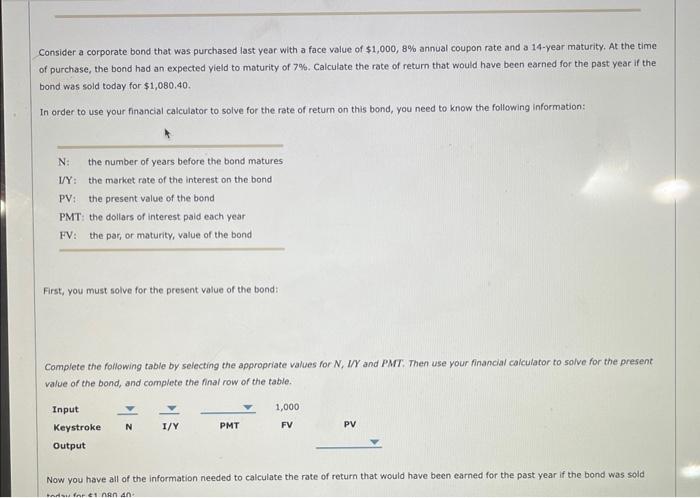
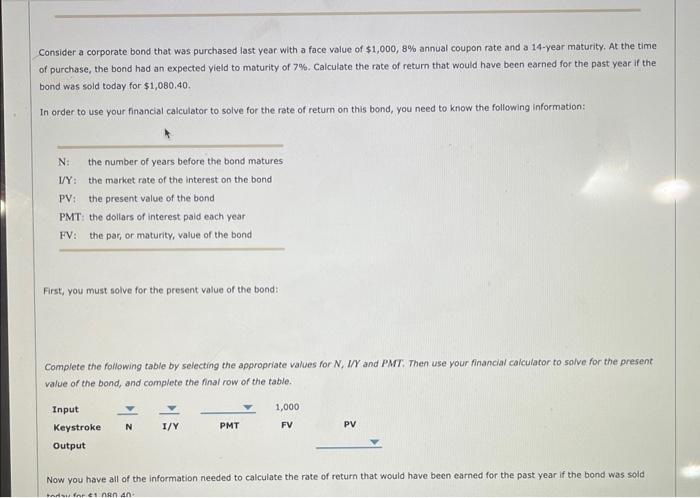
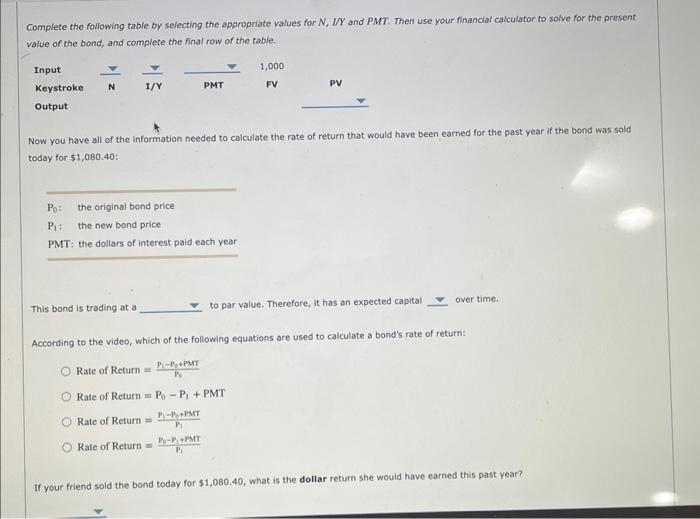
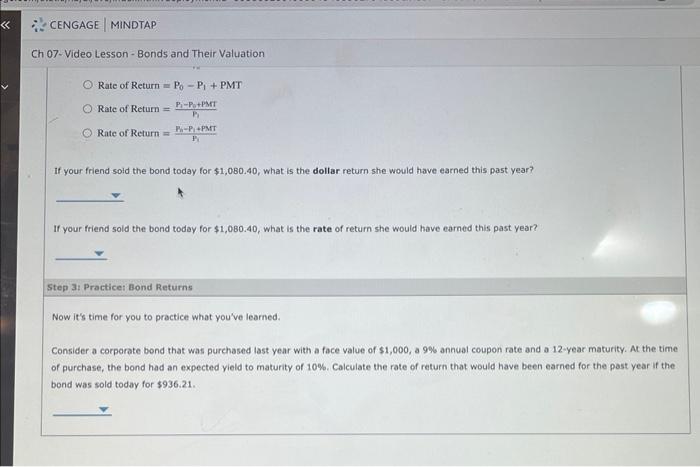
When a coupon bond is issued, the coupon is generally set at a level that causes the bond's market price to equal its par value. If a lower coupon were set, investors would not be willing to pay $1,000 for the bond, but if a higher coupon were set, investors would bid its price up over $1,000. Investment bankers can judge the coupon rate that will cause a bond to sell at its $1,000 par value. A bond that has just been issued is known as a new issue. Once a bond has been issued, it is known as an outstanding bond, or a seasoned issue. Newly issued bonds usually sell at prices dose to par, but the prices of outstanding bonds can vary more or less than par. Coupon payments are constant (excluding floating-rate bonds); so when economic conditions change, a bond with a $70 coupon that sold at its $1,000 par value when it was issued will sell for more or less than $1,000 thereafter. For any given year, this capital gains yieid is calculated as a bond's annual change in price divided by the beginning-of-year price. For example, assuming that market interest rates remain constant at 7%, suppose a bond was selling for $1,000 at the beginning of the year and $1,075 at the end of the year. Its capital gains yield for the year would be $75/$1,000 or 7.5%. Note: If the bond was selling at a premium, its price would decrease over time. Then the capital gains yield would be negative, but it would be offset by a high current yield. A bond's total return is equal to the current yield plus the capital gains yield. In the absence of default risk and assuming market equilibrium, the total return is also equal to M and the market interest rate, which in our example is 7%. Consider the following scenarios: 1. The price of this 7% coupon bond trading at par will remain at $1,000 if the market interest rate remains at 7%. Therefore, its current yield will remain at 7% and its capital gains yield will be zero each year. 2. Suppose the price of the coupon bond is 5% and trades at a discount. At maturity, it must sell at par because that is the amount the company will pay its bondholders. Therefore, its price must rise over time. 3. Suppose the price of the coupon bond is 10% and trades at a premium. At maturity, it must sell at par because that is the amount the company will pay its bondholders. Therefore, its price must decline over time. When a coupon bond is issued, the coupon is generally set at a level that causes the bond's market price to equal its par value. If a lower coupon were set, investors would not be willing to pay $1,000 for the bond, but if a higher coupon were set, investors would bid its price up over $1,000. Investment bankers can judge the coupon rate that will cause a bond to sell at its $1,000 par value. A bond that has just been issued is known as a new issue. Once a bond has been issued, it is known as an outstanding bond, or a seasoned issue. Newly issued bonds usually sell at prices dose to par, but the prices of outstanding bonds can vary more or less than par. Coupon payments are constant (excluding floating-rate bonds); so when economic conditions change, a bond with a $70 coupon that sold at its $1,000 par value when it was issued will sell for more or less than $1,000 thereafter. For any given year, this capital gains yieid is calculated as a bond's annual change in price divided by the beginning-of-year price. For example, assuming that market interest rates remain constant at 7%, suppose a bond was selling for $1,000 at the beginning of the year and $1,075 at the end of the year. Its capital gains yield for the year would be $75/$1,000 or 7.5%. Note: If the bond was selling at a premium, its price would decrease over time. Then the capital gains yield would be negative, but it would be offset by a high current yield. A bond's total return is equal to the current yield plus the capital gains yield. In the absence of default risk and assuming market equilibrium, the total return is also equal to M and the market interest rate, which in our example is 7%. Consider the following scenarios: 1. The price of this 7% coupon bond trading at par will remain at $1,000 if the market interest rate remains at 7%. Therefore, its current yield will remain at 7% and its capital gains yield will be zero each year. 2. Suppose the price of the coupon bond is 5% and trades at a discount. At maturity, it must sell at par because that is the amount the company will pay its bondholders. Therefore, its price must rise over time. 3. Suppose the price of the coupon bond is 10% and trades at a premium. At maturity, it must sell at par because that is the amount the company will pay its bondholders. Therefore, its price must decline over time. In summary, a discount bond has a low coupon rate and a low current yleld, but it has an expected capital gain each year. In contrast, the premium bond has a high current yleld, but it has an expected capital loss each year. True or False: A bond's total return is equal to the current yield plus the capital gains yield. True False Step 2: Learn: Bond Returns Watch the following video for an example, then answer the questions that follow. Consider a corporate bond that was purchased last year with a face value of $1,000,8% annual coupon rate and a 14 -year maturity. At the time of purchase, the bond had an expected yield to maturity of 7%. Calculate the rate of return that would have been earned for the past year if the bond was sold today for $1,080,40. In order to use your financial calculator to solve for the rate of retum on this bond, you need to know the following information: First, you must solve for the present value of the bond: Complete the following table by selecting the appropriate values for N,IY and PMT : Then use your financial calculator to solve for the present value of the bond, and complete the final row of the table. Now you have all of the information needed to calculate the rate of return that would have been earned for the past year if the bond was sold Consider a corporate bond that was purchased last year with a face value of $1,000,8% annual coupon rate and a 14 -year maturity. At the time of purchase, the bond had an expected yield to maturity of 7%. Calculate the rate of return that would have been earned for the past year if the bond was sold today for $1,080,40. In order to use your financial calculator to solve for the rate of retum on this bond, you need to know the following information: First, you must solve for the present value of the bond: Complete the following table by selecting the appropriate values for N,IY and PMT : Then use your financial calculator to solve for the present value of the bond, and complete the final row of the table. Now you have all of the information needed to calculate the rate of return that would have been earned for the past year if the bond was sold Complete the following table by selecting the appropriate values for N,UY and PMT. Then use your financial calculator to solve for the present value of the band, and complete the final row of the table. Now you have all of the information needed to calculate the rate of return that would have been earned for the past year if the bond was sold today for $1,080.40 : This bond is trading at a to par value. Therefore, it has an expected capital over time. According to the video, which of the following equations are used to calculate a bond's rate of return: Rate of Return =T0PiP0+PMT Rate of Return =P0P1+PMT Rate of Return =p1P1P2+PMT Rate of Return =P1PeF1+PMMT If your friend sold the bond today for $1,080.40, what is the dollar return she would have earned this past year? Rate of Return =P0P1+PMT Rate of Return =R1P1P0+PMT Rate of Return =PiPhPi+PMT If your friend sold the bond today for $1,080.40, what is the dollar return she would have earned this past year? If your friend sold the bond today for $1,080.40, what is the rate of return she would have earned this past year? Step 3. Practice: Bond Returns Now it's time for you to practice what you've learned. Consider a corporate bond that was purchased last year with a face value of $1,000,99 annual coupon rate and a 12 -year maturity. At the time of purchase, the bond had an expected yield to maturity of 10%. Calculate the rate of return that would have been earned for the past year if the bond was sold today for $936.21. Rate of Return =P0P1+PMT Rate of Return =R1P1P0+PMT Rate of Return =PiPhPi+PMT If your friend sold the bond today for $1,080.40, what is the dollar return she would have earned this past year? If your friend sold the bond today for $1,080.40, what is the rate of return she would have earned this past year? Step 3. Practice: Bond Returns Now it's time for you to practice what you've learned. Consider a corporate bond that was purchased last year with a face value of $1,000,99 annual coupon rate and a 12 -year maturity. At the time of purchase, the bond had an expected yield to maturity of 10%. Calculate the rate of return that would have been earned for the past year if the bond was sold today for $936.21