Question
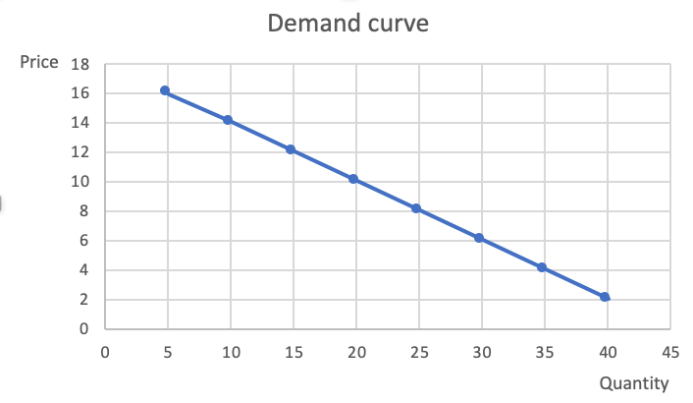
When we estimate a demand curve, we can estimate one that is linear or one that has constant elasticity (the curvy one). It will be
When we estimate a demand curve, we can estimate one that is linear or one that has constant elasticity (the "curvy" one). It will be important to keep the distinction in mind because the coefficients we estimate using the linear specification will be related to the slope and we can use that information to calculate the elasticity at any point on the demand curve as described below. But when we estimate the constant elasticity version (by using the logs of the variables) the coefficients will be THE elasticities - no calculations needed!
The expression below shows how to calculate elasticities at a point on a linear demand curve if you already know the slope. The slope of the demand curve is\frac{\Delta P}{\Delta Q}?Q?P?. When we estimate a linear demand curve, the coefficient we estimate will be \frac{\Delta Q}{\Delta P}?P?Q?(the inverse of the slope of the demand curve). Let\alpha_x?x?represent \frac{\Delta Q}{\Delta P}?P?Q?(this will be the coefficient estimate for a linear demand curve).
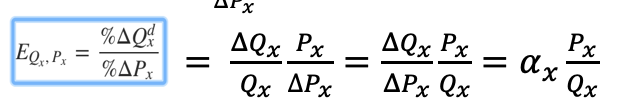
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


