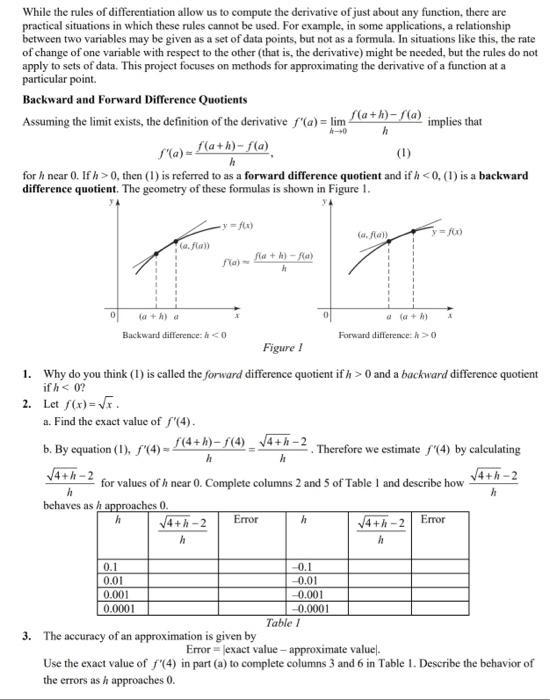
While the rules of differentiation allow us to compute the derivative of just about any function, there are practical situations in which these rules cannot be used. For example, in some applications, a relationship between two variables may be given as a set of data points, but not as a formula. In situations like this, the rate of change of one variable with respect to the other (that is, the derivative) might be needed, but the rules do not apply to sets of data. This project focuses on methods for approximating the derivative of a function at a particular point. Backward and Forward Difference Quotients Assuming the limit exists, the definition of the derivative f'(a) = lim 4-0 f'(a)= f(a+h)-f(a) h (1) for h near 0. If h> 0, then (1) is referred to as a forward difference quotient and if h 0 X Therefore we estimate f'(4) by calculating 4+h-2 4+h-2 Error h Error = exact value-approximate value. Use the exact value of f'(4) in part (a) to complete columns 3 and 6 in Table 1. Describe the behavior of the errors as / approaches 0. Centered Difference Quotients Another formula is used to approximate the derivative of a function at a point is the centered difference quotient (CDQ) f'(a)=f(a+h)-f(a-h) 2h (2) 3. Again consider f(x)=x. a. Draw the graph of f near the point (4, 2) and let h = in the centered difference quotient. Compute and draw the line whose slope is computed by the centered difference quotient and explain why the formula approximates f'(4). Use the CDQ formula to approximate f'(4) by completing Table 2. Give answers accurate to nine decimal places. Approximation b. h Error 0.1 0.01 0.001 0.0001 Table 2 c. Explain why it is not necessary to use negative values of h in Table2. d. In a sentence, compare the accuracy of the derivative estimates in part (b) with those found in Questions 2 and 3. 4. Use the CDQ formula and a table similar to Table 2 to find a good approximation to f'(0) for f (x) = (1 +x)-. Give answers accurate to at least six decimal places. You may use scientific notation to express the error. 5. Use the CDQ formula and a table similar to Table 2 to find a good approximation to f'() for f (x) = sin x. Give answers accurate to at least six decimal places. You may use scientific notation to express the error. 6. Table 3 gives the distance fr) fallen by a smokejumper / seconds after she opens her chute. a. Use the forward difference quotient (Formula 1) with=05 to estimate the velocity of the skydiver at f= 2 s. b. Repeat part (a) using the centered difference quotient (Formula 2). 1 (seconds) Ar) (feet) 0 0 4 15 33 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 Table 3 55 81 109 138 169 Computer Rounding Error Using difference approximations to approximate derivatives with a computer or calculator is prone to rounding errors. These errors occur when a calculator rounds a number before using it in an arithmetic calculation. Such rounding may lead to remarkably inaccurate results. 7. Consider the function f(x) = x0, a. Use analytical methods (i.e. derivative rules) to find the exact value of f'(1). b. Use the forward difference quotient to approximate f'(1) using values h= 102, 103, and 10 Then in a sentence, answer what do you observe? c. Compute approximations to f'(1) using h=10 for n= 5,6,7,... 15. Then in a sentence, answer what do you observe? In Stop Se, you should find that for small mough values of A, the approximations tof'(1) eventually are 0, which is clearly a bad estimate. Here is why this error occurs. Suppose A-1014 The calculator rounds /(1+ 10-14) to 1 and therefore the forward difference quotient becomes ), which is estimated to equal or 0.) 10-1 d. The remedy to rounding errors in this situation is to use small but not too small-values of . Based on the approximations computed in parts (b) and (c), what is a good approximation to f'(1)?