why there is no person answer my question??????????!!!!!!!!!!!!!!!!!!!!!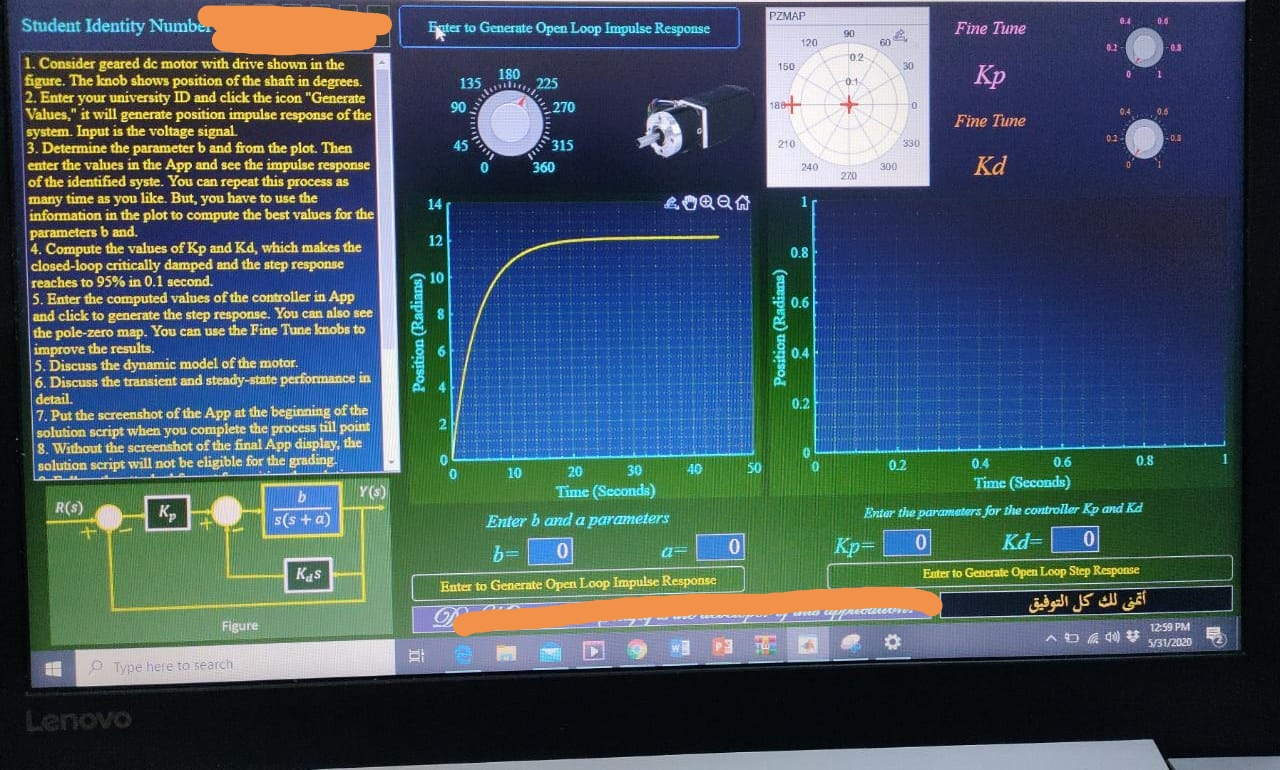

comment:

1. you need to calculate a and b first, then compute Kp and Kd that satisfy 95% when t=0.5.

2. at the first question (Q1) instead of c it is a

PZMAP 6.4 0.6 Student Identity Number Ester to Generate Open Loop Impulse Response 90 Fine Tune 120 02 Os 02 150 30 135 180 11111,,,225 0.1 Kp 90 Hube 270 18+ 0 0,4 0,6 Fine Tune 02 -0.5 45 315 210 330 360 240 300 Kd 270 14 OOM 1 12 0.8 1. Consider geared dc motor with drive shown in the figure. The knob shows position of the shaft in degrees. 2. Enter your university ID and click the icon "Generate Values," it will generate position impulse response of the system. Input is the voltage signal. 3. Determine the parameter b and from the plot. Then enter the values in the App and see the impulse response of the identified syste. You can repeat this process as many time as you like. But, you have to use the information in the plot to compute the best values for the parameters b and 4. Compute the values of Kp and Kd, which makes the closed-loop critically damped and the step response reaches to 95% in 0.1 second. 5. Enter the computed values of the controller in App and click to generate the step response. You can also see the pole-zero map. You can use the Fine Tune knobs to improve the results. 5. Discuss the dynamic model of the motor. 6. Discuss the transient and steady-state performance in detail 7. Put the screenshot of the App at the beginning of the solution script when you complete the process till point 8. Without the screenshot of the final App display, the solution script will not eligible for the grading. 10 0.6 Position (Radians) Position (Radians) 0.4 0.2 0 40 50 0 Y(s) R(S) K b s(s + a 10 20 30 Time (Seconds) Enter b and a parameters b= 0 - 0.2 0.4 0.6 0.8 Time (Seconds) Enter the parameters for the controller Kp and Ka Kp= 0 Kd= 0 Ester to Generale Open Loop Step Response 0 KS Enter to Generate Open Loop Impulse Response 27 = 2 erry: d MANE Figure 12:59 PM Dado 5/31/2020 Type here to search Lenovo 1. Use the impulse response to identify the values of parameter b and c. Write the transfer function, if the input is R(s) and output is the position in radians e(s) 2. Write the transfer function, if the input is R(s) and output is the speed in radians w(s) for the same system. 3. Write the gain of the speed transfer function. 4. Compute the controller parameters, such that the closed-loopis critically damped and the output reaches 95% in 0.5. 5. Discuss the transient behavior of the closed-loop in the given in the Lab2. 6. Discuss the steady-state performance of the closed-loop for the closed-loop given in the Lab2 7. Discuss the sensitivity with respect to the parameters a and kd. 8. What can be the source of noise in the original plot? 9. If we want to control the speed of the motor shaft, such that the steady-state error for the ramp-function is zero and the closed- loop transfer function has no derivative term in the numerator. Sketch the closed-loop and write the transfer function using the symbolic parameters. There is no need to compute the numerical values of the parameters. PZMAP 6.4 0.6 Student Identity Number Ester to Generate Open Loop Impulse Response 90 Fine Tune 120 02 Os 02 150 30 135 180 11111,,,225 0.1 Kp 90 Hube 270 18+ 0 0,4 0,6 Fine Tune 02 -0.5 45 315 210 330 360 240 300 Kd 270 14 OOM 1 12 0.8 1. Consider geared dc motor with drive shown in the figure. The knob shows position of the shaft in degrees. 2. Enter your university ID and click the icon "Generate Values," it will generate position impulse response of the system. Input is the voltage signal. 3. Determine the parameter b and from the plot. Then enter the values in the App and see the impulse response of the identified syste. You can repeat this process as many time as you like. But, you have to use the information in the plot to compute the best values for the parameters b and 4. Compute the values of Kp and Kd, which makes the closed-loop critically damped and the step response reaches to 95% in 0.1 second. 5. Enter the computed values of the controller in App and click to generate the step response. You can also see the pole-zero map. You can use the Fine Tune knobs to improve the results. 5. Discuss the dynamic model of the motor. 6. Discuss the transient and steady-state performance in detail 7. Put the screenshot of the App at the beginning of the solution script when you complete the process till point 8. Without the screenshot of the final App display, the solution script will not eligible for the grading. 10 0.6 Position (Radians) Position (Radians) 0.4 0.2 0 40 50 0 Y(s) R(S) K b s(s + a 10 20 30 Time (Seconds) Enter b and a parameters b= 0 - 0.2 0.4 0.6 0.8 Time (Seconds) Enter the parameters for the controller Kp and Ka Kp= 0 Kd= 0 Ester to Generale Open Loop Step Response 0 KS Enter to Generate Open Loop Impulse Response 27 = 2 erry: d MANE Figure 12:59 PM Dado 5/31/2020 Type here to search Lenovo 1. Use the impulse response to identify the values of parameter b and c. Write the transfer function, if the input is R(s) and output is the position in radians e(s) 2. Write the transfer function, if the input is R(s) and output is the speed in radians w(s) for the same system. 3. Write the gain of the speed transfer function. 4. Compute the controller parameters, such that the closed-loopis critically damped and the output reaches 95% in 0.5. 5. Discuss the transient behavior of the closed-loop in the given in the Lab2. 6. Discuss the steady-state performance of the closed-loop for the closed-loop given in the Lab2 7. Discuss the sensitivity with respect to the parameters a and kd. 8. What can be the source of noise in the original plot? 9. If we want to control the speed of the motor shaft, such that the steady-state error for the ramp-function is zero and the closed- loop transfer function has no derivative term in the numerator. Sketch the closed-loop and write the transfer function using the symbolic parameters. There is no need to compute the numerical values of the parameters