With our rocket successfully launched, we need to determine where its targetMarsis. This problem was solved by Kepler by supposing the planet has a circular orbit instead of an elliptical one and then correcting for the actual orbits eccentricity. Kepler derived the following equation (which is appropriately named Keplers equation):

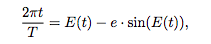
where t is time, T is the orbital period, E(t) is an angle (in radians) called the eccentric anomaly, and e is the eccentricity of the orbit. The eccentric anomaly is the angular position of the planet when projected onto the supposed circular orbit and changes with time. Unfortunately, this equation cannot be solved for E(t) analytically, so we must rely on numerical means. We would like our probe to arrive at Mars in 183 days. Write a MATLAB script (or scripts, if you would like to separate them) to determine the eccentric anomaly for t = 183 days four times:

a) with the bisection method;

b) with the false-position method;

c) with the Newton-Raphson method;

d) with the secant method.

Use T = 687 days for Mars orbital period and e = 0.0934 for the orbits eccentricity. Use percent relative error as the stopping criterion, with s = 106% for each part.

2nt -= E(t) -e-sin( E(t )), 2nt -= E(t) -e-sin( E(t ))