with these test case

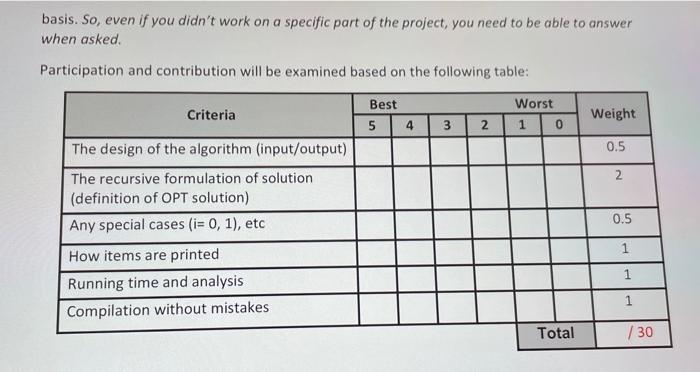


2. Problem description - Your chance to win big! The College of Engineering invites students like you to participate in a game where you can use your expertise in algorithm design to win lots of money! The setting is as follows: There are n stages in the game in which you are given access to n blue doors and a red doors, During each stage you get to open either the red or the blue door IH Behind each door there is an amount which you can win (if positive) or loose (if negative). Your goal is to choose the doors correctly so that you maximize your earnings. The following rules are imposed by the administration: The game proceeds in stages. So, doors must be opened in the order 1, 2, 3, -- and you can always select either the red or the blue door (but not both). In stage 1, you have to open one of the two doors. However, it is ok if you decide to not select any door in some later stage. - Once you make a selection, next time you must switch color. So, if you picked a red door in the current stage, then in the next one you must pick a blue door (and vice versa). Your goal is to come up with a Dynamic Programming algorithm to solve this problem, subject to the constraints mentioned above. For example, consider the door values shown below: 9 Stage 1 2 3 4 5 6 7 Red 1 -2 -1 4 2 9 -2 Blue 7 1 5 36 Then you can select the shaded doors for a total sum of 7-1+9+9=24 You should implement a Dynamic programming algorithm for this problem, test it for correctness using the test instances that can be found in the class web page and evaluate its performance. 3. Project Implementation You can work in teams of up to two. The teams are expected to accomplice the following goals. Implement your algorithms in JAVA or Python following the conventions below. ON is the number of doors o Redt), Blue are the arrays of maximum size 10000 holding the amounts behind each o The amounts are integers in the range - 1000 to 1000 When your program is called, it should print the maximum sum attained as well as the doors that were selected at the various stages O. For the example above, your program should print Maximum sum: 24 Doors selected: B1, R3, B4, R6 door 0 basis. So, even if you didn't work on a specific part of the project, you need to be able to answer when asked. Participation and contribution will be examined based on the following table: Criteria Best 5 4 Worst 1 0 Weight 3 2 0.5 2 0.5 The design of the algorithm (input/output) The recursive formulation of solution (definition of OPT solution) Any special cases (i= 0, 1), etc How items are printed Running time and analysis Compilation without mistakes 1 1 Total /30 . Project report (70%) O O O Organization and sectioning of the report. Small introduction about the problem you are trying to solve. Detailed design steps including formulation of the DP recurrence, explanation on how you arrived to it. Proof of correctness and justifications for any choices made. Analysis of the DP algorithm in terms of running time and space requirements, o Testing and screenshots along with a verbal description of the results. O Conclusions. References. Source code with proper comments. Check the report rubric posted in the web page to know what we expect in the report. N = 3 red] = { 2, 4, -15}; blue = {-18, -17, -12}; - Maximum sum: 2 Doors selected: R1 2 2 2 2 2 2 2 2 2 2 N = 3 red[= {5, -3, 3}; blue] = { 2, -2, -3}; Maximum sum: 6 Doors selected: R3 B2 R1 2 2 2 2 2 2 ( 2 2 2 2 2 2 ( 2 2 2 N = 5 red] = {10, -14, 6, -7, -3}; blue = {-6, -6, 19, -6, 9}; = Maximum sum: 31 Doors selected: B5 R4 B3 R1










