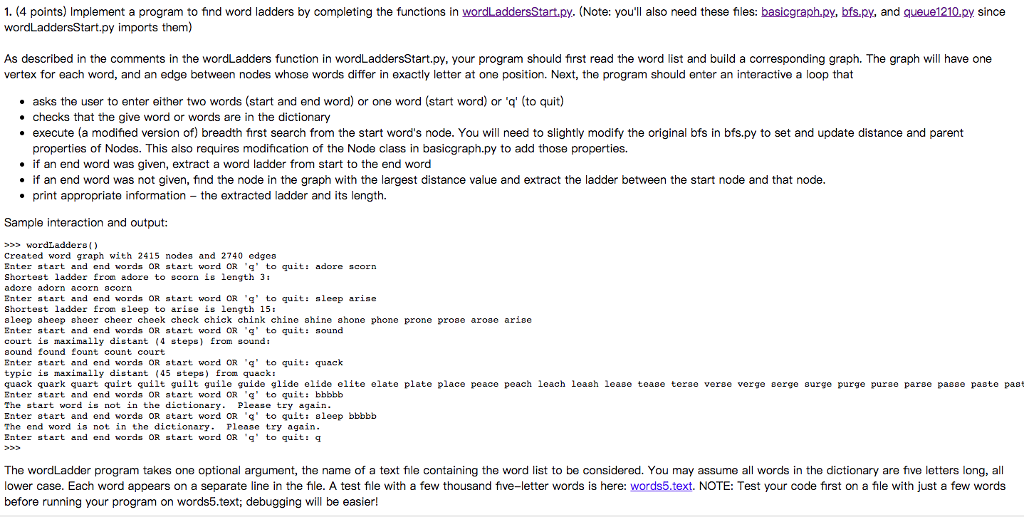
############# wordLaddersStart.py from basicgraph import * from bfs import * # return True if there should be an edge between nodes for word1 and word2 # in the word graph. Return False otherwise # def shouldHaveEdge(word1, word2): return False # Give a file of words, return a graph with # - one node for each word # - an edge for every pair of words, w1 and w2, # where shouldHaveEdge(w1, w2) is True. # def buildWordGraph(wordsFile = "words5.text"): wordGraph = Graph() return wordGraph # Assumption: (modified) breadth first search has already been executed. # # Thus, parent values have been set in all nodes reached by bfs. # Now, work backwards from endNode (end word) to build a list of words # representing a ladder between the start word and end word. # # For example, if the start word was "cat" and the end word was "dog", after bfs # we might find that "dog"'s parent was "dot" and then that "dot"'s parent was # "cot" and finally that "cot"'s parent was "cat" (which has no parent). Thus, # a ladder from "cat" to "dog" is ["cat", "cot", "dot", "dog"] # # Return [] if the endNode has no parent. If the end node has no parent, the # the breadth first search could not reach it from the start node. Thus, there # is no word ladder between the start and end words. # def extractWordLadder(endNode): ladder = [] return ladder def wordLadders(wordsFile = "words5.text"): # 1. read the words file # 2. build a graph based on the words file # 3. user interaction loop: # - request user to enter either two words (start and end word) # or one word (start word) or 'q' (to quit) # - check that the give word or words are in the dictionary # - execute breadth first search from the start word's node # (Note: you need to slightly modify the original bfs in bfs.py # to set and update distance and parent properties of Nodes. This also # requires modification of the Node class in basicgraph.py to add # those properties.) # - if an end word was given, extract word ladder from # start to that endword # - if an end word was not given, find the node in the graph # with the largest distance value and extract the ladder between # the start node and that node. # - print appropriate information - the extracted ladder and its length # code for 1. and 2. above goes here # code for 3. goes inside the while loop below userInput = input("Enter start and end words OR start word OR 'q' to quit: ") words = userInput.split() while (words[0] != 'q'): userInput = input("Enter start and end words OR start word OR 'q' to quit: ") words = userInput.split() 

############## basicgraph.py

# Class to represent nodes (vertices) of a graph # class Node(object): # name must be a string def __init__(self, name): self.name = name self.status = 'unseen' def getName(self): return self.name def getStatus(self): return self.status # should be one of 'unseen', 'seen', 'processed' def setStatus(self, status): self.status = status def __repr__(self): return "".format(self.name) # Class for representing undirected graphs, i.e. graphs in which edges # have no direction - if there is an edge between a and b, # you can "move" from a to b and/or from b to a # class Graph(): #nodes is a list of the nodes in the graph # # edges is a list of two-tuples (n1, n2). If there is an edge between n1 and n2, either (n1, n2) # or (n2, n1) will be in the list of edges # # adjacencyLists is a dictionary with the set of nodes as the set of keys. For each node, n1, # adjacencyLists[n1] is a list of the nodes n2 such that (n1,n2) is an edge. # i.e. it is a list of all nodes to which n1 is connected directly by an edge. # def __init__(self): self.nodes = [] self.edges = [] self.adjacencyLists = {} def addNode(self, node): if node in self.nodes: raise ValueError("node is already in graph. You can't add it again.") else: self.nodes.append(node) self.adjacencyLists[node] = [] # To add an edge between node1 and node2, node1 and node2 must already be in the graph def addEdge(self, node1, node2): if node1 == node2: raise ValueError("edges to self are not allowed in undirected graphs") if not((node1 in self.nodes) and (node2 in self.nodes)): raise ValueError("at least one node of given edge is not in the graph") if node2 in self.adjacencyLists[node1]: raise ValueError("edge is already in graph. You can't add it again.") self.edges.append((node1, node2)) self.adjacencyLists[node1].append(node2) self.adjacencyLists[node2].append(node1) def neighborsOf(self, node): return self.adjacencyLists[node] def getNode(self, name): for node in self.nodes: if node.getName() == name: return node return None def hasNode(self, node): return node in self.nodes def hasEdge(self, node1, node2): return node2 in self.adjacencyLists[node1] def __repr__(self): result = "[Graph with: Nodes:" for node in self.nodes: result = result + " " + str(node) result = result + " Edges: " result = result + ', '.join([(edge[0].getName() + '-' + edge[1].getName()) for edge in self.edges]) + ']' return result def genGraph(): n1 = Node("NYC") n2 = Node("Miami") g = Graph() print(g) g.addNode(n1) g.addNode(n2) print(g) g.addEdge(n1, n2) print(g) return g def genCompleteGraph(n): nodes = [] g = Graph() for i in range(n): g.addNode(Node(str(i))) nodes = g.nodes for n1 in nodes: for n2 in nodes: if (n1 != n2) and (not g.hasEdge(n1, n2)): g.addEdge(n1,n2) return g import random # return a new list with the same elements as input L but randomly rearranged def mixup(L): newL = L[:] length = len(L) for i in range(length): newIndex = random.randint(i,length-1) newL[newIndex], newL[i] = newL[i], newL[newIndex] return(newL) def genRandomGraph(numNodes, numEdges): nodes = [] edges = [] g = Graph() for i in range(numNodes): g.addNode(Node(str(i))) allPairs = [] for i in range(numNodes): for j in range(i+1, numNodes): allPairs.append((str(i),str(j))) allPairs = mixup(allPairs) edgesAdded = 0 while edgesAdded  
 
 
############## bfs.py
 
from queue1210 import * from basicgraph import * ##### # # classic Breadth First Search # # See, e.g., http://en.wikipedia.org/wiki/Breadth-first_search # def bfs(graph, startNode): for n in graph.nodes: n.setStatus('unseen') startNode.setStatus('seen') print("Initializing queue with: ", startNode.name) queue = Queue() queue.enqueue(startNode) while queue.size() != 0: print(queue) currentNode = queue.dequeue() print("removed {} from queue. Processing neighbors".format(currentNode.name)) for node in graph.neighborsOf(currentNode): if node.getStatus() == 'unseen': node.setStatus('seen') queue.enqueue(node) currentNode.setStatus('processed')
 
 
 
############### queue1210.py 
 
class Queue: # We represent an empty queue using an empty list def __init__(self): self.q = [] # Return True if there are no items in the queue. Return False otherwise. def isEmpty(self): return (len(self.q) == 0) # Add an item to the rear of the queue. def enqueue (self, item): self.q.append(item) # If the queue is not empty, remove and return the queue's front item # If the queue is empty, generate an error or print(a message and return None. def dequeue (self): if self.isEmpty(): raise ValueError("dequeue invoked on empty Queue") else: result = self.q[0] # Note that this is O(n). Okay for use in CS1210 BUT use # a better implementation if you will do many dequeues on # very big queue! (Python's collections.deque provides a good # implementation) self.q = self.q[1:] return result # Return the number of items currently in the queue def size(self): return(len(self.q)) def __repr__(self): return "queue{front: " + str(self.q)[1:-1] + " :end}" def testQueue(): q = Queue() print("Created an empty Queue") print("Size is now: {}".format(q.size())) print("Enqueue-ing: 3, then 'hi', then 99") q.enqueue(3) q.enqueue("hi") q.enqueue(99) print("Size is now: {}".format(q.size())) print("Dequeue-ing ...") print(q.dequeue()) print("Size is now: {}".format(q.size())) print("Dequeue-ing ...") print(q.dequeue()) print("Size is now: {}".format(q.size())) print("Enqueue-ing: [1,2]") q.enqueue([1,2]) print("Size is now: {}".format(q.size())) print("Dequeue-ing ...") print(q.dequeue()) print("Size is now: {}".format(q.size())) print("Dequeue-ing ...") print(q.dequeue()) print("Size is now: {}".format(q.size())) 
  1. (4 points) Implement a program to find word ladders by completing the functions in wordLaddersStart py. (Note: you'll also need these files: basicgraph.py, bfs.py, and queue1210,py since wordLaddersStart.py imports them) As described in the comments in the wordLadders function in wordLaddersStart.py, your program should first read the word list and build a corresponding graph. The graph will have one vertex for each word, and an edge between nodes whose words differ in exactly letter at one position. Next, the program should enter an interactive a loop that . asks the user to enter either two words (start and end word) or one word (start word) or 'q' (to quit) . checks that the give word or words are in the dictionary . execute (a modified version of) breadth first search from the start word's node. You will need to slightly modify the original bfs in bfs.py to set and update distance and parent properties of Nodes. This also requires modification of the Node class in basicgraph.py to add those properties. . if an end word was given, extract a word ladder from start to the end word . if an end word was not given, find the node in the graph with the largest distance value and extract the ladder between the start node and that node. . print appropriate information the extracted ladder and its length. Sample interaction and output: wordLaddere) Created word graph with 2415 nodes and 2740 edges Enter start and end words OR start word OR to quit: adore scorn Shortest ladder froa adore to scorn ie length 3 adore adorn acorn acorn Enter st?rt ?nd end words OR start word OR g, to quit: sleep arise Shortest ladder Eroa sleep to arise ie length 15 aleep aheep sheer cheer cheek check chick chink chine shine ahone phone prone proae aroae arise Enter start and end words OR start word OR 'q, to quit: sound court is maximally distant (4 steps) from sound Bound found fount count court Enter start and end words OR start word OR to quit: quack typic is maximally distant (45 steps) Erom quack: quack quark quart quirt quilt guilt guile guide glide elide elite elate plate place peace peach leach leaah lease tease terse verse verge eerge aurge purge purae paree paase paste past Ent?r at rt nnd end word 0R start word OR The start word is not in the dictionary Please try again Enter atart and end worda OR start word OR to quit: Bleep bbbbb The end word is not in the dictionary Enter start and end words OR start word OR to quit: q to quit: bbbbb The wordLadder program takes one optional argument, the name of a text file containing the word list to be considered. You may assume all words in the dictionary are five letters long, all lower case. Each word appears on a separate line in the file. A test file with a few thousand five-letter words is here: words5.text. NOTE: Test your code first on a file with just a few words before running your program on words5.text; debugging will be easier!  1. (4 points) Implement a program to find word ladders by completing the functions in wordLaddersStart py. (Note: you'll also need these files: basicgraph.py, bfs.py, and queue1210,py since wordLaddersStart.py imports them) As described in the comments in the wordLadders function in wordLaddersStart.py, your program should first read the word list and build a corresponding graph. The graph will have one vertex for each word, and an edge between nodes whose words differ in exactly letter at one position. Next, the program should enter an interactive a loop that . asks the user to enter either two words (start and end word) or one word (start word) or 'q' (to quit) . checks that the give word or words are in the dictionary . execute (a modified version of) breadth first search from the start word's node. You will need to slightly modify the original bfs in bfs.py to set and update distance and parent properties of Nodes. This also requires modification of the Node class in basicgraph.py to add those properties. . if an end word was given, extract a word ladder from start to the end word . if an end word was not given, find the node in the graph with the largest distance value and extract the ladder between the start node and that node. . print appropriate information the extracted ladder and its length. Sample interaction and output: wordLaddere) Created word graph with 2415 nodes and 2740 edges Enter start and end words OR start word OR to quit: adore scorn Shortest ladder froa adore to scorn ie length 3 adore adorn acorn acorn Enter st?rt ?nd end words OR start word OR g, to quit: sleep arise Shortest ladder Eroa sleep to arise ie length 15 aleep aheep sheer cheer cheek check chick chink chine shine ahone phone prone proae aroae arise Enter start and end words OR start word OR 'q, to quit: sound court is maximally distant (4 steps) from sound Bound found fount count court Enter start and end words OR start word OR to quit: quack typic is maximally distant (45 steps) Erom quack: quack quark quart quirt quilt guilt guile guide glide elide elite elate plate place peace peach leach leaah lease tease terse verse verge eerge aurge purge purae paree paase paste past Ent?r at rt nnd end word 0R start word OR The start word is not in the dictionary Please try again Enter atart and end worda OR start word OR to quit: Bleep bbbbb The end word is not in the dictionary Enter start and end words OR start word OR to quit: q to quit: bbbbb The wordLadder program takes one optional argument, the name of a text file containing the word list to be considered. You may assume all words in the dictionary are five letters long, all lower case. Each word appears on a separate line in the file. A test file with a few thousand five-letter words is here: words5.text. NOTE: Test your code first on a file with just a few words before running your program on words5.text; debugging will be easier