Workings needed
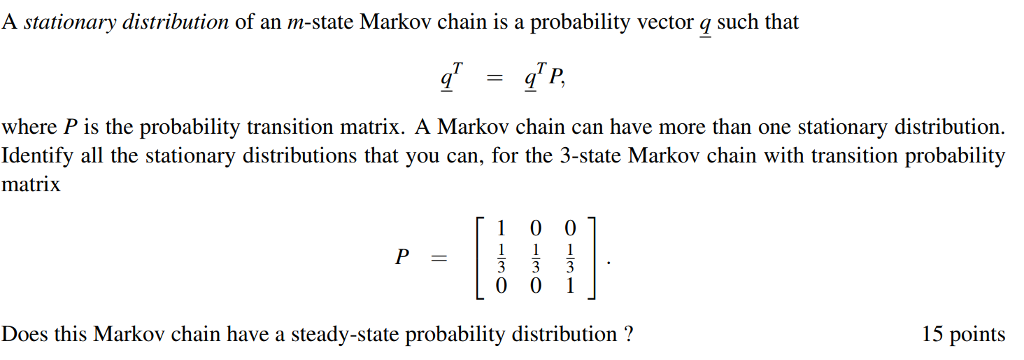
What does the univariate t test tell you that the bivariate correlation test alone does not? What does the bivariate test tell you that the univariate test does not tell you? Select one: Only the univariate comparison tells you that vanilla is preferred over chocolate on average; only the bivariate analysis tells you that people who prefer vanilla more also prefer chocolate more. Only the univariate comparison tells you how to predict chocolate preference from vanilla preference; only the bivariate analysis tells you that people who prefer vanilla more also prefer chocolate more. Only the univariate comparison tells you that people who prefer vanilla more also prefer chocolate more; only the bivariate analysis tells you that chocolate is preferred over vanilla on average Only the univariate comparison tells you that the preferences for chocolate and vanilla are not different; only the bivariate analysis tells you that people who prefer vanilla more also prefer chocolate more.Consider a Markov chain {Xn, n = 0, 1, . ..} on the state space S = {0, 1, 2}. Suppose that the Markov chain has the transition matrix 2 10 10 10 2 P = 3 10 2 4 10 10 1. Show that the Markov chain has a unique stationary mass. 2. Let h denote the stationary mass of the Markov chain. Find h(x) for all x E S. 3. Show that the Markov chain has the steady state mass. 4. Let h* denote the steady state mass of the Markov chain. Find h*(x) for all x E S.A stationary distribution of an m-state Markov chain is a probability vector q such that = q P, where P is the probability transition matrix. A Markov chain can have more than one stationary distribution. Identify all the stationary distributions that you can, for the 3-state Markov chain with transition probability matrix O O P Owl Does this Markov chain have a steady-state probability distribution ? 15 points1. Write the dual for each of the following primal problems: Maximize u = -5x1 + 2x2 Minimize z = 6x1 + 3x2 Subject to: Subject to: -xitx2 s -2 6x1 - 3x2 + X3 2 2 2x1 + 3x2 $5 3x1 + 4x2 + X3 25 X1, X2 2 0 X1,X2,X3 20 Maximize u = -x1 + 2x2 - 3x3 Subject to: X1 - X2 5 -2 2x1 + X2 - X3 2 15 Xz + X3 = 10 X1, X2 2 0 X3 unrestricted 2. Find the optimal value of the objective function for the following problem by inspecting only its dual. Do not solve the dual by the simplex method. Explain how you found the answer. Minimize z = 10x1 + 4x2 + 5X3 Subject to: 5x1 - 7x2 + 3x3 2 50 X1,X2, X3 20 3. Consider the following set of inequalities. Note that X1 = X2 = 0 is not a feasible solution. A feasible solution can be found by using the trivial objective function (maximize z = x1 + X2) with the constraints and then solving the dual, from which a solution for the set of inequalities can be found. Find a feasible point with this method (show your work). 2x1 + 3x2 $ 12 -3x1 + 2x2 5-4 3x1 - 5x2 $ 2 x1 unrestricted; x2 2 0 . Consider the following LP. Use the dual problem to show that the basic solution with (x1, *2) = (0,0) is not optimal. Explain why. Maximize z = 2x1 + 4x2 + 4x3 - 3x4 Subject to: X1 + X2 + X3 = 4 X1 + 4x2 + X4 = 8 X1, X2, X3, X4 2 0