Write a function in MATLAB to compute the coefficients for a cubic spline interpolating function and then to use the coefficients to compute a cubic spline interpolating polynomial. We will focus on natural splines. Do not use built-in MATLAB functions for cubic spines.

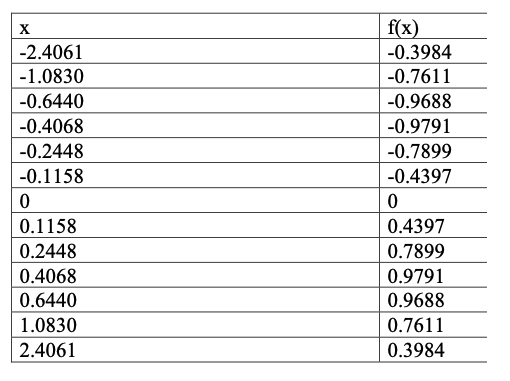
Compute and graph the natural cubic spline interpolant for the data shown in the table below. To plot, use linspace(-2.4,2.4,100).

PSEUDOCODE:

The function given in the table above is: f(x) = x/(.25+x^2) . Use the cubic spline interpolant you found above to approximate the function at the uniformly spaced grid points z=linspace(-2,2,10). What is the maximum error for the cubic spline interpolant? How does the result compare to that predicted by the theoretical error estimate?

\begin{tabular}{|l|l} \hline x & f(x) \\ \hline2.4061 & 0.3984 \\ \hline1.0830 & 0.7611 \\ \hline0.6440 & 0.9688 \\ \hline0.4068 & 0.9791 \\ \hline0.2448 & 0.7899 \\ \hline0.1158 & 0.4397 \\ \hline 0 & 0 \\ \hline 0.1158 & 0.4397 \\ \hline 0.2448 & 0.7899 \\ \hline 0.4068 & 0.9791 \\ \hline 0.6440 & 0.9688 \\ \hline 1.0830 & 0.7611 \\ \hline 2.4061 & 0.3984 \\ \hline \end{tabular} INPUT X=(x0,,xn),Y=(f(x0),,f(xn))=(a0,,an), OUTPUT aj,bj,cj,dj for j=0,..,n1 the coefficients, where the cubic spline is: S(x)=Sj(x)=aj+bj(xxj)+cj(xxj)2+dj(xxj)3, for xjxxj+1. STEP 1. For i=0,1,n1 hi=xi+1xi End For STEP 2. For i=1,n1 i=hi3(ai+1ai)hi13(aiai1) End For STEP 3. Set \%STEPS 3, 4, 5 and part of 6 solve the tridiagonal linear system. l0=10=0z0=0 STEP 4. For i=1,n1 li=2(xi+1xi1)hi1i1i=hi/lizi=(ihi1zi1)/li End For STEP 5. Set ln=1zn=0cn=0 STEP 6. For j=n1,n2,,0 cj=zjjcj+1bj=(aj+1aj)/hjhj(cj+1+2cj)/3dj=(cj+1cj)/(3hj) End For STEP 7. OUTPUT aj,bj,cj,dj for j=0,..,n1 STOP