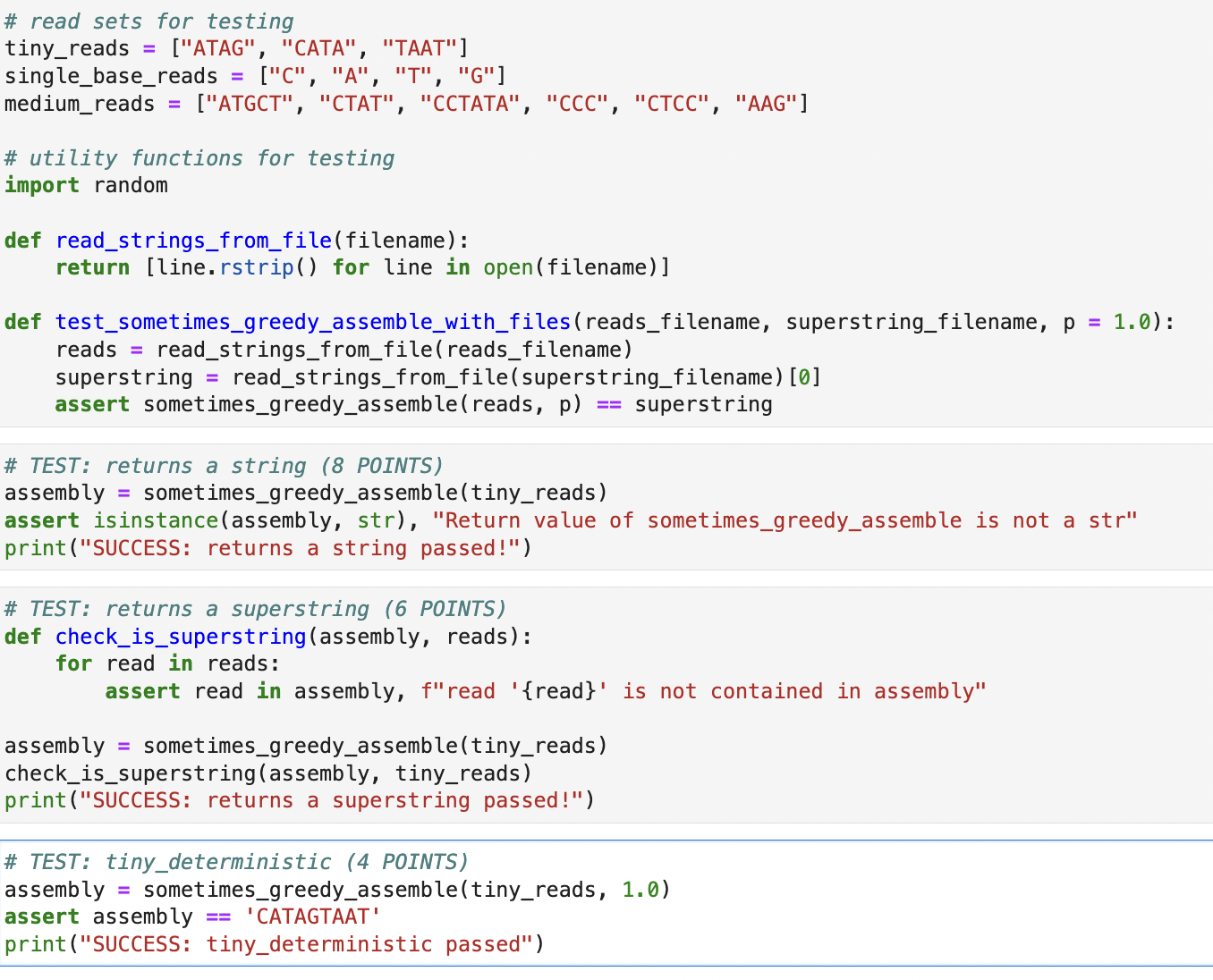
Write a function, sometimes_greedy_assemble, that takes as input a list of read strings and uses a modified version of the greedy fragment assembly algorithm to assemble them into a single superstring. We will consider a modification to the greedy algorithm described for fragment assembly (Page 9 of the Sequence Assembly - Graphs and fragment assembly) in which the algorithm does not always add the next (largest overlap) compatible edge from the queue. Instead, after popping the next edge off of the queue and checking that it is compatible with the current graph, we will choose to add it to the graph with probability p, and if not, we will instead add it to a list, H, of "held aside" edges that will be considered later, and then continue with the algorithm. The modified pseudocode for the algorithm is: Let G be a graph with fragments as vertices and no edges Create a queue, Q, of overlap edges (not currently in G), with edges in order of increasing weight (decreasing overlap length) Initialize H to be an empty list While G is disconnected Pop the next possible edge e = (u, v) off of Q If outdegree(u) = 0 and indegree(v) = 0 and e does not create a cycle o Let x be a random number drawn uniformly from [0, 1) o If x < p o add e to G o move the edges in H back to Qin sorted order o Else o add e to H If Q is empty o move the edges in H back to Qin sorted order A potential advantage of this randomized algorithm is that, in cases where the deterministic greedy algorithm fails to find the shortest superstring, there is a non-zero probability that the randomized algorithm will find a shorter superstring than the deterministic algorithm. And we can run the randomized algorithm many times to increase these chances. To keep things simple for this homework we will allow overlaps of any length (including zero). In practice, we would typically require some minimum overlap length. For simplicity, we will also assume that: 1. we are assembling a single-stranded sequence and 2. that no read is a substring of any other read. Important implementation details Random number generation Random number generation should occur only at the line specified in the pseudocode, and you should use the random.random function for this purpose. Tie-breaking criteria For the purpose of making this algorithm deterministic, we must establish tiebreaking criteria for edges in the overlap graph that have the same weight. For two edges with the same weight, we will first choose the edge whose source vertex read is first in lexicographical order. If the source vertices are identical, then we choose the edge whose target vertex read is first in lexicographical order. For example, if e1 = ATCGGAGGAT and e2 = ATCGGAGGAA, we will attempt to use edge e2 first because GGAA # read sets for testing tiny_reads = ["ATAG", "CATA", "TAAT"] single_base_reads = ["C", "A", "T", "G"] medium_reads = # utility functions for testing import random ["ATGCT", "CTAT", "CCTATA", "CCC", "CTCC", "AAG"] def read_strings_from_file(filename): return [line.rstrip () for line in open (filename)] def test sometimes_greedy_assemble_with_files (reads_filename, superstring_filename, p = 1.0): reads = read_strings_from_file(reads_filename) superstring assert sometimes_greedy_assemble (reads, p) = read_strings_from_file(superstring_filename) [0] # TEST: returns a string (8 POINTS) assembly = sometimes_greedy_assemble(tiny_reads) # TEST: returns a superstring (6 POINTS) def check_is_superstring (assembly, reads): for read in reads: assembly = assert isinstance (assembly, str), "Return value of sometimes_greedy_assemble is not a str" print("SUCCESS: returns a string passed!") == = assert read in assembly, f" read '{read}' is not contained in assembly" sometimes_greedy_assemble (tiny_reads) check_is_superstring(assembly, tiny_reads) print("SUCCESS: returns a superstring passed!") superstring # TEST: tiny_deterministic (4 POINTS) assembly sometimes_greedy_assemble(tiny_reads, 1.0) assert assembly == 'CATAGTAAT' print("SUCCESS: tiny_deterministic passed")