Write a program, or modify an earlier one, to once more calculate the value of the integral 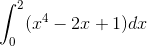from Example (5.28), using the trapezoidal rule with 20 slices, but this time have the program also print an estimate of the error on the result, calculated using the method of Eq. (5.28). To do this you will need to evaluate the integral twice, once with N1 = 10 slices and then again with N2 = 20 slices. Then Eq. (5.28) gives the error. How does the error calculated in this manner compare with a direct computation of the error as the difference between your value for the integral and the true value of 4.4? Why do the two not agree perfectly?

Simpson's rule: (a) Write a program to calculate an value for the integral f(x4 2x + 1) dx from Ex- ample 5.1, but using Simpson's rule with ten slices instead of the trapezoidal rule. (b) Run the program and compare your result to the known correct value of 4.4. What is the fractional error on your calculation? (c) Modify the program to use a hundred slices instead, then a thousand. Note the improvement in the result. How do the results compare with those from Example 5.1 for the trapezoidal rule with the same number of slices