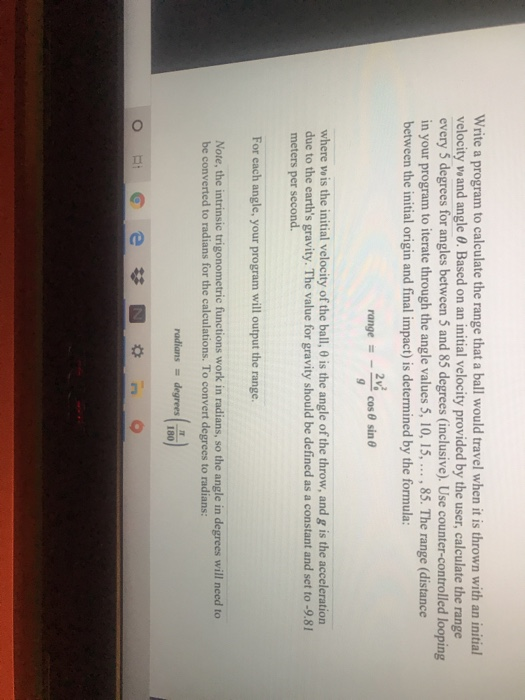
Write a program to calculate the range that a ball would travel when it is thrown with an initial

velocity

v

0

and angle

. Based on an initial velocity provided by the user, calculate the range

every 5 degrees for angles between 5 and 85 degrees (inclusive). Use counter-controlled looping

in your program to iterate through the angle values 5, 10, 15, ... , 85. The range (distance

between the initial origin and final impact) is determined by the formula:

where

v

0

is the initial velocity of the ball, is the angle of the throw, and

g

is the acceleration

due to the earth's gravity. The value for gravity should be defined as a constant and set to -9.81

fortran program

its coding ( program to calculate ball range using counter - control looping to iterate through the angle value)

u can write it by hand

Write a program to calculate the range that a ball would travel when it is thrown with an initial velocity wand angle 0. Based on an initial velocity provided by the user, calculate the range every 5 degrees for angles between 5 and 85 degrees (inclusive). Use counter-controlled looping in your program to iterate through the angle values 5, 10, 15, ..., 85. The range (distance between the initial origin and final impact) is determined by the formula: range = - = cos sin e where is the initial velocity of the ball, is the angle of the throw, and g is the acceleration due to the earth's gravity. The value for gravity should be defined as a constant and set to -9.81 meters per second. For each angle, your program will output the range. Note, the intrinsic trigonometric functions work in radians, so the angle in degrees will need to be converted to radians for the calculations. To convert degrees to radians: radians = degrees Write a program to calculate the range that a ball would travel when it is thrown with an initial velocity vo and angle 0. Based on an initial velocity provided by the user, calculate the range every 5 degrees for angles between 5 and 85 degrees (inclusive). Use counter-controlled looping in your program to iterate through the angle values 5, 10, 15, ..., 85. The range (distance between the initial origin and final impact) is determined by the formula: 2V coses range = - cos sin 9 where vois the initial velocity of the ball, is the angle of the throw, and g is the acceleration due to the earth's gravity. The value for gravity should be defined as a constant and set to -9.81 meters per second. For each angle, your program will output the range. Note, the intrinsic trigonometric functions work in radians, so the angle in degrees will need to be converted to radians for the calculations. To convert degrees to radians: radians = degrees (180)