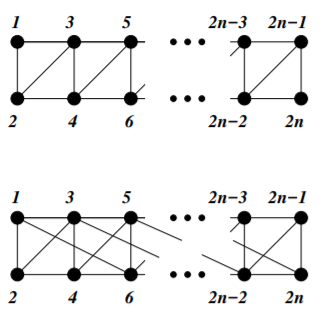
Write a program to solve the graph k-coloring problem with the following twist. A good coloring must have the standard property that it assigns different colors to the vertices of each edge but, in addition, it also has to have the following property: if two vertices have a common neighbor then they must be colored differently. Use your program and the clasp solver to find the smallest number of colors for which the coloring of the type given above exists for the following two graphs (in each case, for n = 30). You can accomplish this by trying values of k successively starting with k = 2. The first value k for which clasp returns an answer is the solution. Build a representation of the graphs by hand, or write a program to generate it.

1 3 5 2n-3 2n-1 60 2n-2 2n 5 2n-3 2n-1 21- 2n-2 2n 1 3 5 2n-3 2n-1 60 2n-2 2n 5 2n-3 2n-1 21- 2n-2 2n