Write a Python function called midpoint(f, t0, yvec0, b, n) that implements the Midpoint Method for a system of 2 equations.

* Approximate the solution to 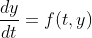, y(t₀) = y₀

* The first step with step size h is t₁ = t₀ + h and y₁ = y₀ + h f(t₀,y₀)

* Start at (t₀, y₀) and find the slope f(t₀, y₀)

* Find the halfway interval [t₀, t₁] by t_1/2 = t₀ + h/2 and y_1/2 = y₀ + h/2 f(t₀, y₀)

* Evaluate the slope at f(t_1/2, y_1/2)

* Take a step along [t₀, t₁] using the slope t₁ = t₀ + h and y₁ = y₀ + h f(t_1/2, y_1/2)

Next we want to use the midpoint method: If we have the system

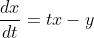and 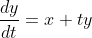we want to generate the points (t_i, (x_i, y_i))

* Treat y = (x, y) as a vector so that f(t, y) = (tx - y, x + ty)

* Let the solution to y be a list yvec = [x, y] and implement f(t, yvec) as:

def f(t, yvec):

return [t * yvec[0] - yvec [1], yvec [0] + t.* yvec[1]]

The function should return a list of t values and a list of y values. When you return the next list, it should have the form

yvec = [[x_0, y_0] , [x_1, y_1] , ... , [x_n, y_n]]

Test the code with 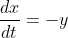and 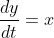where x(0) = 1, y(0) = 0, x(t) = cos t, y(t) = sin t

dy dt = f(ty) dc =tx - y dt dy dt = c+ty dc = -4 -Y dt dy = 2 dt dy dt = f(ty) dc =tx - y dt dy dt = c+ty dc = -4 -Y dt dy = 2 dt