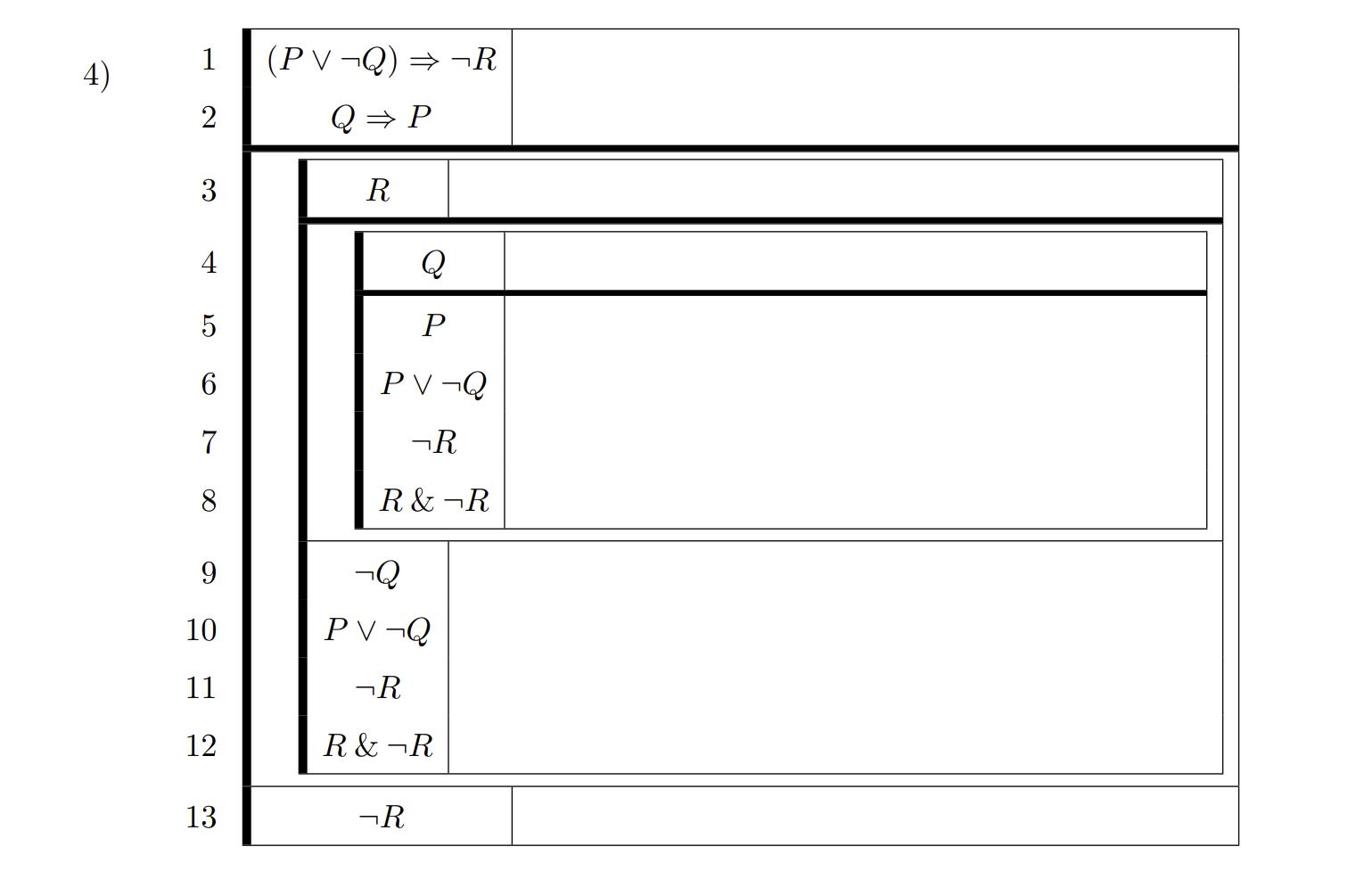
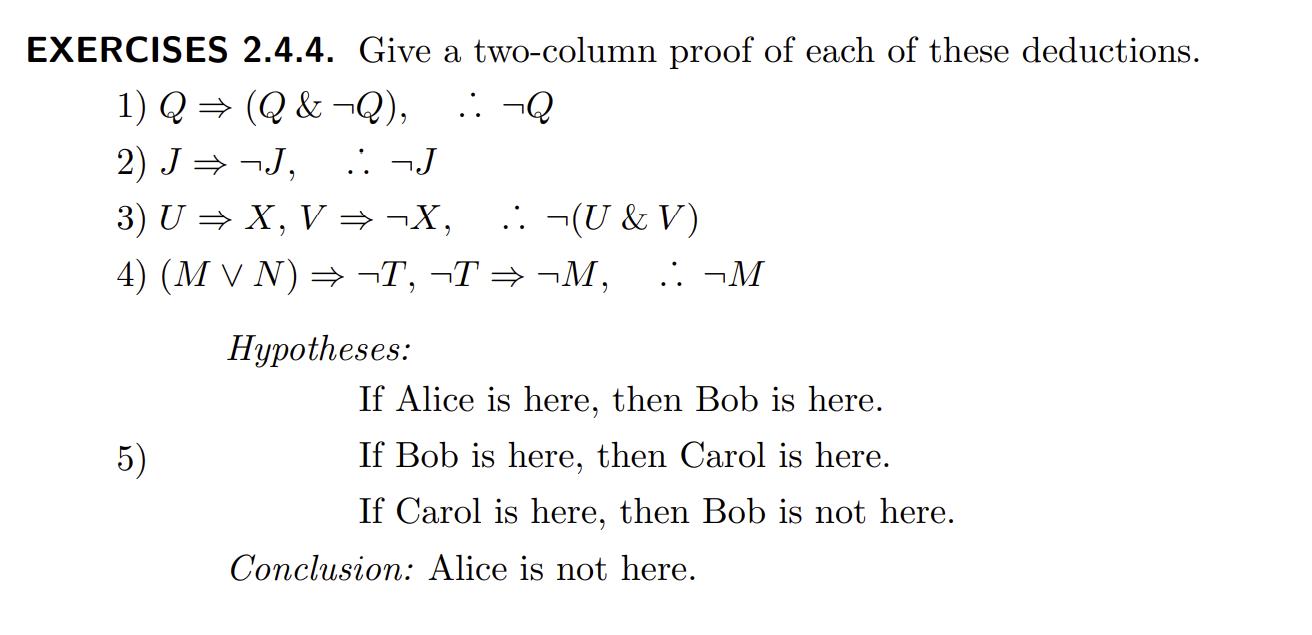
Write a two-column proof of each of the following deductions: :: P S 1) P (Q V R), QS, R S, 2) Q (Q P), .: Q P 3) MV (N M), 4) R (R(R(RQ))), R=(QVP) 5) AV B, A C, B D, C E, D E, Hypotheses: :: M N . E The Pope is here if and only if the Queen is here. The Queen is here if and only if the Registrar is here. Conclusion: The Pope is here if and only if the Registrar is here. 7) 8) 9) Hypotheses: If Jim is sick, he should stay in bed. If Jim is not sick, he should go outside to play. Conclusion: Jim should either stay in bed or go outside to play. Hypotheses: If the King will sing, then the Queen will sing. If the King and the Queen will both sing, then the Prince and the Princess will also sing. If the King and the Queen and the Prince and the Princess will all sing, then the party will be fun. Conclusion: If the King will sing, then the party will be fun. Hypotheses: If the Pope is here, then either the Queen is here or the Registrar is here. If the Queen is here, then the Spy is here. If the Registrar is here, then the Spy is here. Conclusion: If the Pope is here, then the Spy is here. EXERCISES 2.4.3. Provide a justification (rule and line numbers) for each line of these proofs. 1) 1 2 3 4 LO 5 6 7 8 9 10 CBVC A &B C BVC B -B B&B C C (A &B) C 2) 3) 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 (A v B) B B AV B B B&B B P Q QR R P P Q R -P P& P -P 4) 1 2 3 4 5 6 7 8 9 10 11 12 13 (PVQ) R Q P R P PV-Q R R&R -Q PV-Q R R&R R 5) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Z (C & N) Z (N &C) (NVC) N NVC (NVC) & (NVC) -N C NVC (NVC) & (NVC) C Z C & N C C & C Z N &C N N & N (NVC) NVC EXERCISES 2.4.4. Give a two-column proof of each of these deductions. 1) Q (Q & Q), :: Q 2) JJ, :: J 3) UX, V X, .: (U & V) 4) (M V N) T, TM, .. M Hypotheses: 5) If Alice is here, then Bob is here. If Bob is here, then Carol is here. If Carol is here, then Bob is not here. Conclusion: Alice is not here. EXERCISE 2.5.2. Give a two-column proof of the deduction A (B & C), A, .. C Work backwards from what you want. The ultimate goal is to derive the conclusion. Look at the conclusion and ask what the introduction rule is for its main logical operator. This gives you an idea of where you want to be just before the last line of the proof. Then you can treat this line as if it were your goal; we call it a subgoal because it represents partial progress toward the true goal. Ask what you could do to derive the subgoal. For example: If your conclusion is A & B, then you need to figure out a way to prove A and a way to prove B. If your conclusion is a conditional A B, plan to use the -intro rule. This requires starting a subproof in which you assume A. In the subproof, you want to derive B. The last of the four mazes in Exercise 2.5.1 is easy if you work backwards from the finish, instead of forward from the start. EXERCISE 2.5.3. Give a two-column proof of the deduction (P VQ) (R & S), (RV S) (P & Q), .. P Q Try breaking the proof down into cases. If it looks like you need an additional hypothesis (A) to prove what you want, try considering two cases: since AVA is a tautology ("Law of Excluded Middle"), it suffices to prove that A andA each yield the desired conclusion. EXERCISE 2.5.4. Give a two-column proof of the deduction P Q, P R, (Q V R) S, .. S Look for useful subgoals. Working backwards is one way to identify a worthwhile sub- goal, but there are others. For example, if you have A B, you should think about whether you can obtain A somehow, so that you can apply -elimination. EXERCISE 2.5.7. Give a two-column proof of the deduction PQ, QP, : P Repeat as necessary. After you have made some progress, by either deriving some new assertions or deciding on a new goal that would represent substantial progress, see what the above strategies suggest in your new situation. Persist. Try different things. If one approach fails, try something else. When solving a difficult maze, you should expect to have to backtrack several times, and the same is true when doing proofs. EXERCISES 2.5.8. Give a two-column proof of each of these deductions. 1) (P & Q) (QV R), .. (P& Q) (RVS) 2) P (QV R), Q-P, RS, P S