Write the Lagrangian and use Lagrange's Equations to derive the equations of motion for each of the four systems shown in the figure.  In each case, also derive an expression for the generalized momenta, write the Hamiltonian, and derive Hamilton's Equations of motion.  Show that the latter are equivalent to those obtained by Lagrange's Equations.

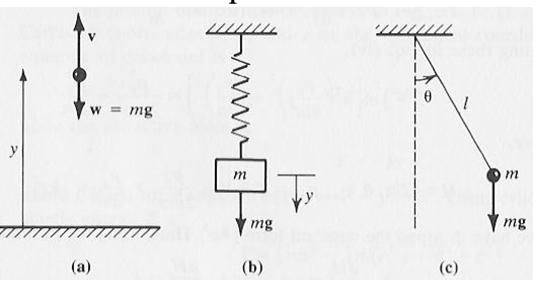
A mass m is shot vertically upward in a uniform gravitational field.

A mass m is tied to a spring of spring constant k and is allowed to vibrate vertically in a uniform gravitational field. 

A simple pendulum of mass m and length l is swinging in a vertical plane in a uniform

gravitational field. 

A mass m moves along the x-axis and is subject to a conservative force given by

F(x) = -kx  + 8x³,  where k and  8 are positive constants. 

w = mg (a) m mg (b) (c) 1 m mg