Write the program in C or JAVA only.

In this assignment you will write a program that will retrieve a polynomial expression, two initial values, and associated parameters from command line arguments specified below, and then exercise the Newton and Secant Methods to attempt to find a root within the required accuracy and within the maximum number of iterations. The program must generate output to the console (terminal) screen as specified below.

Command Line Arguments

1. Your program must compile and run from the command line.
2. The program executable must be named newton (all lower case, no spaces or file extension).
3. The program must retrieve the following command line arguments, which must be specified in the order shown below. Your program may NOT prompt the user to enter any input values, NOR may it simply wait for the user to enter such values without prompting.

Argument 1:	p0	an integer or decimal real value, which can be negative; this value represents the initial x-value for Newtons Method and the first initial value for the Secant Method.
Argument 2:	p1	an integer or decimal real value, which can be negative; this value represents the second initial x-value for the Secant Method.
Argument 3:	tol	a decimal real value, which must be positive; this value represents the accuracy tolerance value (e.g., .0005).
Argument 4:	max	a positive integer; represents the maximum number of iterations that each method will be allowed to run.
Argument 5:	lim	a positive integer; represents the highest order term of the input polynomial (e.g., lim = 3 for a cubic polynomial).
Arguments 6 to (6+lim)		decimal real values for the coefficients of the terms of the polynomial, in descending order of the powers of x, from x^lim to x^0.

Specifying the Polynomial Using Input Arguments

To simplify input of the polynomial, for this assignment the polynomial will be specified by entering its coefficients as decimal real values in descending order of the powers of x, from x^lim to x^0, where the following conditions must be observed:

(a) An implicit coefficient of 1 must be included explicitly; and

(b) All terms of the polynomial must be specified, so that terms that do not appear in the polynomial must be represented by zero (0) coefficients in the parameter set.

For example, suppose we wish to enter the function x³ - 2x² - 5. For this function, the x¹ term is not used. Also, this function has an implicit coefficient of 1 for the x³ term. The parameter set for this function will be: 1 -2 0 -5 .

Please note that the number of parameters needed to specify the polynomial will vary and will always be one more than the degree of the polynomial. For the third order polynomial above, we have four coefficients. For a 4^th degree polynomial, 5 coefficients are needed, etc.

Running the Program

To run the program, simply launch the program from a command prompt or terminal window and enter all of the required parameters, in the order specified above, following the name of the program before pressing the "enter" or "return" key on your keyboard.

For a Java program in Windows, Mac OS, or Linux, an example run command (with arguments) would be:

java newton 2 4 .0005 50 3 1 -2 0 -5

For a C version of the program in Mac OS or Linux, the run command would look like

.ewton 2 4 .0005 50 3 1 -2 0 -5

And the C version in Windows would be simply:

newton 2 4 .0005 50 3 1 -2 0 -5

Please note that all of the command arguments are separated by spaces and are entered immediately after the program name and before you press the "enter" or "return" key.

Program Output

The program must send all output to the console (terminal) screen. The output must contain the following sections and must be formatted in substantially the same form as the sample output in the next section:

(a) Program title with your name: The program must output "Polynomial Root Finder by [ your name ]"

(b) Echo control parameters: The program must echo the input parameters for p0, p1, tol, max, and lim.

(c) Echo polynomial: The program must echo the polynomial coefficients in a manner that associates each coefficient with the power of x that it precedes. Additionally, negative values should be expressed as such. The x⁰ term may be displayed with or without the x⁰.

(d) Report Newton Method Results: The program must show the values of each successive approximation computed in accordance with Newtons Method. Do not format the output values (we wish to view all digits). The program must also report whether or not a solution was found, and if so, after how many iterations. The program must also detect a possible divide by zero situation and exit gracefully with an appropriate message in such situation.

(e) Report Secant Method Results: The program must show the values of each successive approximation computed in accordance with the Secant Method. Do not format the output values (we wish to view all digits). The program must also report whether or not a solution was found, and if so, after how many iterations. The program must also detect a possible divide by zero situation and exit gracefully with an appropriate message in such situation.

Sample Output

The following is the desired output from running the program using the following command line parameters: 2 4 .0005 50 3 1 -2 0 -5. The function for this output is f(x) = x³ -2x² -5. The graph of this function looks like:

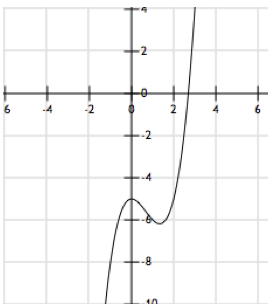
from which we can see that the function has a root somewhere between 2 and 3.

The program output for the above parameter set is:

Please note how the terms of the polynomial are shown. This is the recommended display format.

Program Testing

Your program will be tested by running a number of test cases. Some of the test cases will share the same function but will vary the other parameters. Different functions will also be tested. Scenarios that should be trapped for divide-by-zero errors by both methods will also be tested.

4 -2 4 -4 201