You are given a checkerboard with n rows and n columns. This is just a nn table V . The (i, j) entry of V has value v(i, j) (can be positive or negative). We want to move a checker from the top-left corner (i.e., position (1, 1)) to the bottom-right (i.e., position (n, n)). The only legal moves are to move a checker down by one square, right by one square, or diagonally down-right by one square. The value of a sequence of moves is the sum of the values of the entries in the sequence. We want the maximum value of any legal sequence of moves. Here is an example of a 3 3 checkerboard:

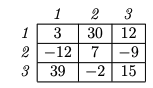
The sequence of moves (1, 1) (1, 2) (2, 2) (3, 3) is legal and has total value 3 + 30 + 7 + 15 = 55. Give a dynamic programming algorithm that given the values V determines the maximum value of any legal sequence of moves from (1, 1) to (n, n). You just need to output the total value from the optimal solution. (Faster (and correct) algorithm in O() notation is worth more credit.) (a) Define the entries of your table in words. E.g., T(i) is ..., or T(i, j) is .... (b) State the recurrence for the entries of your table in terms of smaller subproblems. (c) Write pseudocode for your algorithm to solve this problem. (d) Analyze the running time of your algorithm.

1 2 3 1 3 30 30 12 2-12 7 -9 3 39 -215