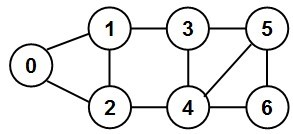
You are given the code of graph implementation in which the information of the neighbors of the nodes (i.e., the adjacency list) is stored as an array of linked lists. The code for the List class, implemented as a Singly Linked List, is also given. Note that the implementation assumes the vertices are labeled from 0 to N-1, where N is the number of vertices in the graph. Your tasks in this project are to: (i) add member functions to the List class and the Graph class so that we could find the degree (the number of neighbors) for any node in the graph (ii) after implementing the required member functions, add code in the main function to print the degrees of the vertices in the graph as well as compute and print the probability of finding vertices with a certain degree (ranging from 1 to N-1, where N is the number of vertices in the graph) and the average degree of the vertices in the given graph based on these probabilities (computed as the weighted average of the number of vertices with the possible degree values, as shown in the slides). Test your code with a connected graph of 10 vertices or more such that the degree of any vertex is at least 1 and is at most N-1 (where N is the number of vertices in the graph). The edgeList is passed as input to your program. The edges of a graph (edgeList) are stored as an ordered pair of vertices with the ID of the first vertex in the pair being always less than the ID of the second vertex in the pair. For example, the edgeList for the graph below is shown alongside.

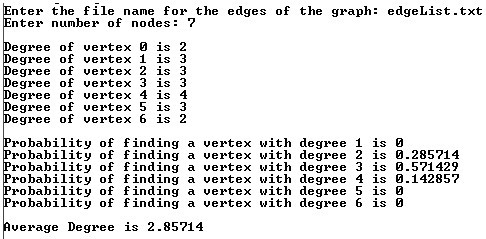
A sample screenshot of the output for the above 7-vertex graph is shown below. Your code should generate a similar output for your test graph of 10 or more vertices.

Code.cpp

#include

#include

#include

#include

#include

#include

#include

#include

#include // for string tokenizer and c-style string processing

using namespace std;

// implementing the dynamic List ADT using Linked List

class Node {

private:

int data;

Node* nextNodePtr;

public:

Node() {}

void setData(int d) {

data = d;

}

int getData() {

return data;

}

void setNextNodePtr(Node* nodePtr) {

nextNodePtr = nodePtr;

}

Node* getNextNodePtr() {

return nextNodePtr;

}

};

class List {

private:

Node * headPtr;

public:

List() {

headPtr = new Node();

headPtr->setNextNodePtr(0);

}

Node* getHeadPtr() {

return headPtr;

}

bool isEmpty() {

if (headPtr->getNextNodePtr() == 0)

return true;

return false;

}

void insert(int data) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

while (currentNodePtr != 0) {

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

}

Node* newNodePtr = new Node();

newNodePtr->setData(data);

newNodePtr->setNextNodePtr(0);

prevNodePtr->setNextNodePtr(newNodePtr);

}

void insertAtIndex(int insertIndex, int data) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != 0) {

if (index == insertIndex)

break;

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

index++;

}

Node* newNodePtr = new Node();

newNodePtr->setData(data);

newNodePtr->setNextNodePtr(currentNodePtr);

prevNodePtr->setNextNodePtr(newNodePtr);

}

int read(int readIndex) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != 0) {

if (index == readIndex)

return currentNodePtr->getData();

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

index++;

}

return -1; // an invalid value indicating

// index is out of range

}

void modifyElement(int modifyIndex, int data) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

int index = 0;

while (currentNodePtr != 0) {

if (index == modifyIndex) {

currentNodePtr->setData(data);

return;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

index++;

}

}

void deleteElementAtIndex(int deleteIndex) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

Node* nextNodePtr = headPtr;

int index = 0;

while (currentNodePtr != 0) {

if (index == deleteIndex) {

nextNodePtr = currentNodePtr->getNextNodePtr();

break;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

index++;

}

prevNodePtr->setNextNodePtr(nextNodePtr);

}

void deleteElement(int deleteData) {

Node* currentNodePtr = headPtr->getNextNodePtr();

Node* prevNodePtr = headPtr;

Node* nextNodePtr = headPtr;

while (currentNodePtr != 0) {

if (currentNodePtr->getData() == deleteData) {

nextNodePtr = currentNodePtr->getNextNodePtr();

break;

}

prevNodePtr = currentNodePtr;

currentNodePtr = currentNodePtr->getNextNodePtr();

}

prevNodePtr->setNextNodePtr(nextNodePtr);

}

void IterativePrint() {

Node* currentNodePtr = headPtr->getNextNodePtr();

while (currentNodePtr != 0) {

cout getData()

currentNodePtr = currentNodePtr->getNextNodePtr();

}

cout

}

// add any required member function here

};

class Graph {

private:

int numNodes;

List* adjacencyList;

public:

Graph(int n) {

numNodes = n;

adjacencyList = new List[numNodes];

}

void addEdge(int u, int v) {

adjacencyList[u].insert(v);

adjacencyList[v].insert(u);

}

List getNeighborList(int id) {

return adjacencyList[id];

}

// add any required member function here

};

int main() {

string graphEdgesFilename;

cout

cin >> graphEdgesFilename;

int numNodes;

cout

cin >> numNodes;

Graph graph(numNodes);

ifstream graphEdgeFileReader(graphEdgesFilename);

if (!graphEdgeFileReader) {

cout

return 0;

}

int numCharsPerLine = 25;

char *line = new char[numCharsPerLine];

// '25' is the maximum number of characters per line

graphEdgeFileReader.getline(line, numCharsPerLine, ' ');

// ' ' is the delimiting character to stop reading the line

while (graphEdgeFileReader) {

char* cptr = strtok(line, " ");

string uNodeToken(cptr);

int uNodeID = stoi(uNodeToken);

cptr = strtok(NULL, " ");

string vNodeToken(cptr);

int vNodeID = stoi(vNodeToken);

graph.addEdge(uNodeID, vNodeID);

graphEdgeFileReader.getline(line, numCharsPerLine, ' ');

}

cout

// add code here to find and print the probabilities of finding vertices with certain degree

// and compute the average degree based on these probabilities

system("pause");

return 0;

}

Edges File

0 1

0 2

1 2

1 3

2 4

3 4

3 5

4 5

4 6

5 6