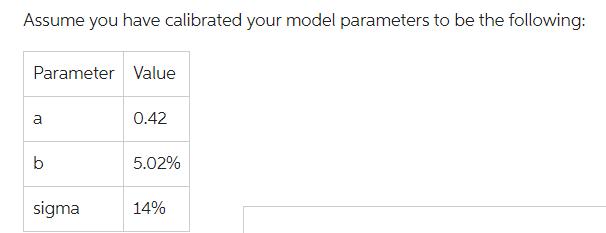
You are using the Cox-Ingersoll-Ross model of equilibrium yield curve changes, described by: dr = a*(b-r)*dt + o*sqrt(r)*dz Assume you have calibrated your model parameters to be the following: Parameter Value a b sigma 0.42 5.02% 14% And that the current short term rate is r = 3.58%. Assume further that the random values of dz for the next two periods produced by your RNG are -0.25 and 0.44. Under these conditions, what would be the short term interest rate two years from now.