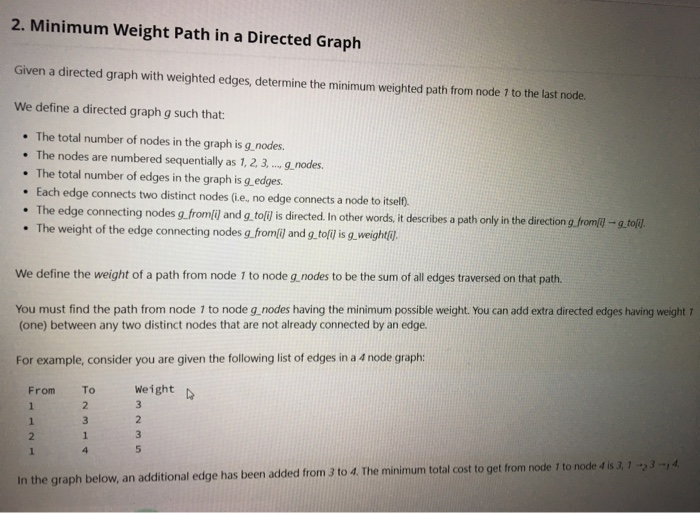
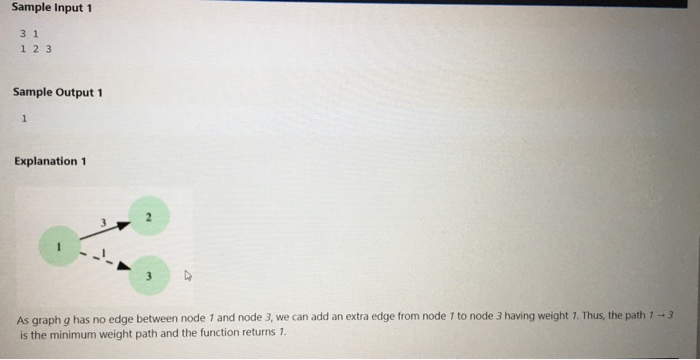
2. Minimum Weight Path in a Directed Graph Given a directed graph with weighted edges, determine the minimum weighted path from node 7 to the last node. We define a directed graph g such that: The total number of nodes in the graph is g_nodes. The nodes are numbered sequentially as 1, 2, 3,... g_nodes. The total number of edges in the graph is g_edges. Each edge connects two distinct nodes (i.e, no edge connects a node to itself). The edge connecting nodes g_from[i] and g_to[i] is directed. In other words, it describes a path only in the direction g_from[il-g_toli]. The weight of the edge connecting nodes g_from[i] and g_tofi] is g_weight[i]. We define the weight of a path from node 1 to node g_nodes to be the sum of all edges traversed on that path. You must find the path from node 1 to node g_nodes having the minimum possible weight. You can add extra directed edges having weight 7 (one) between any two distinct nodes that are not already connected by an edge. For example, consider you are given the following list of edges in a 4 node graph: Weight 3 From 1 1 2 1 To 2 3 1 4 235 In the graph below, an additional edge has been added from 3 to 4. The minimum total cost to get from node 7 to node 4 is 3, 1-23-14 In the graph below, an additional edge has been added from 3 to 4. The minimum total cost to get from node 1 to node 4 is 3, 1-23-14. Function Description 2 Complete the function minCost in the editor below. The function must return an integer denoting the minimum possible weight of any path from node 7 to node g_nodes. 5 minCost has the following parameter(s): g_nodes: the integer number of nodes in graph g Constraints g_from[g_from[1]....g_from[n]]: an array of integers representing edge origin nodes g_to[g_to[1]...g_to[n]]: an array of integers representing edge target nodes g_weight(g_weight[1]...g weight[n]): an array of integers representing edge weights . . 3 sg.nodes s 10 1sg edges s min(104, (anodes (g.nodes - 1sg_weight(i) s 106 Sample Input 1 31 123 Sample Output 1 1 Explanation 1 3 As graph g has no edge between node 7 and node 3, we can add an extra edge from node 7 to node 3 having weight 7. Thus, the path 1-3 is the minimum weight path and the function returns 1.