You can use Matlab for the lower-level mechanics, such as inverting and manipulating matrices, performing differentiation (for checking so- lutions) and integrations, and for determining eigenvalues. Dont use Matlab to determine eigenvectors or directly solve ODEs. Do explain how each problem is worked, what you have actually done in Matlab, and provide a copy of any program (script) used.
Please help me out with the problem (c) only using Matlab.
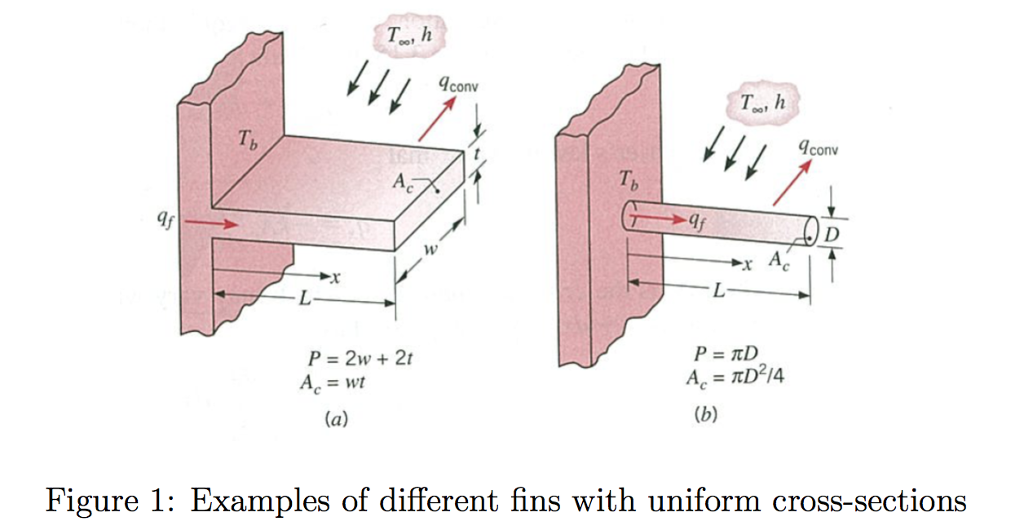
E. Determine the steady temperature distribution in a cooling fin that has a uniform cross-section. Assuming the fin is relatively thin in comparison to the length, we can represent the temperature as solely a function of distance from the base (see Fig. 1 for two examples Let T(x) represent the temperature of the fin as a function of the length from its base, To the temperature at the base, and Too the temperature of the surrounding air. The cross-sectional area and perimeter are A and P respectively, k is the thermal conductivity, and h the heat transfer coefficient. With an energy balance and Fouriers law, we obtain th equation and boundary conditions for the temperature e following differential dT Ph dr2 Aik T(0)To CO dx Do the followin g: (a) Determine the corresponding differential equation and boundary con- ditions for the dimensionless temperature (T-100)/(Z-Too) and position z = x/L. Make the substitutions g-hL/k and b-hPL2/Ak. (b) Solve this second-order differential equation. Verify that your solution s correct (c) Plot the dimensionless temperatures for two situations: (b,g) = (1,1) and (b, g) = (10,10) E. Determine the steady temperature distribution in a cooling fin that has a uniform cross-section. Assuming the fin is relatively thin in comparison to the length, we can represent the temperature as solely a function of distance from the base (see Fig. 1 for two examples Let T(x) represent the temperature of the fin as a function of the length from its base, To the temperature at the base, and Too the temperature of the surrounding air. The cross-sectional area and perimeter are A and P respectively, k is the thermal conductivity, and h the heat transfer coefficient. With an energy balance and Fouriers law, we obtain th equation and boundary conditions for the temperature e following differential dT Ph dr2 Aik T(0)To CO dx Do the followin g: (a) Determine the corresponding differential equation and boundary con- ditions for the dimensionless temperature (T-100)/(Z-Too) and position z = x/L. Make the substitutions g-hL/k and b-hPL2/Ak. (b) Solve this second-order differential equation. Verify that your solution s correct (c) Plot the dimensionless temperatures for two situations: (b,g) = (1,1) and (b, g) = (10,10)
