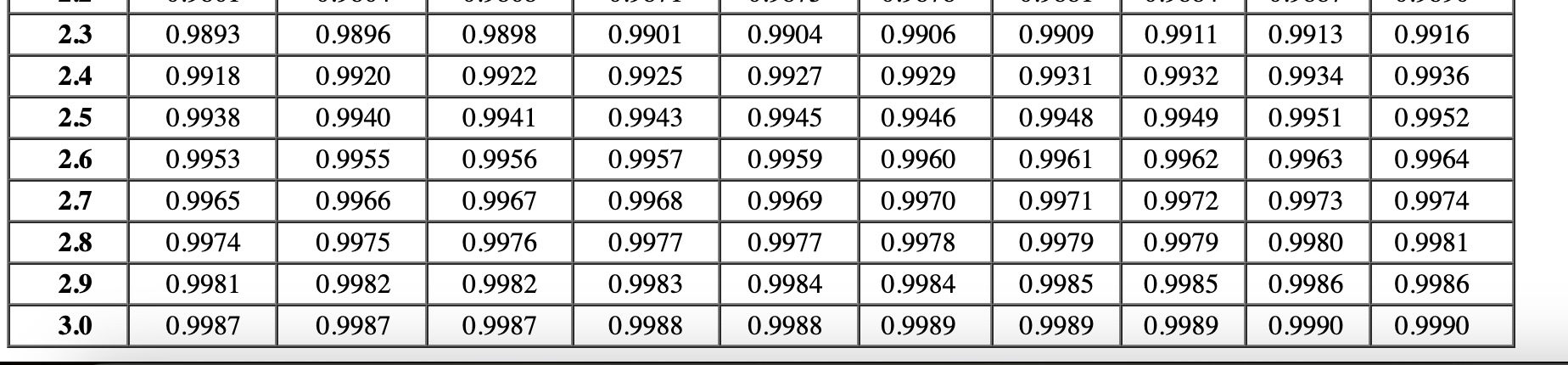
You have a one-time chance to purchase an item for $7. The item can be sold to customers for $34. After one day, the item has no salvage value because it becomes rotten at the end of the day. It will then cost you $13 per item to properly dispose of any unsold items. You think you can sell 1,200 units in one day, but you also know that the standard deviation of demand for the item is 50 units. Use Appendix A.

How many units should you order?

Note: Round your intermediate calculations to 2 decimal places and final answer to the nearest whole number.

Table of Cumulative Probability of the Normal Distribution (one-tail) \begin{tabular}{|l|l|l|l|l|l|l|l|l|l|l|} \hline 2.3 & 0.9893 & 0.9896 & 0.9898 & 0.9901 & 0.9904 & 0.9906 & 0.9909 & 0.9911 & 0.9913 & 0.9916 \\ \hline 2.4 & 0.9918 & 0.9920 & 0.9922 & 0.9925 & 0.9927 & 0.9929 & 0.9931 & 0.9932 & 0.9934 & 0.9936 \\ \hline 2.5 & 0.9938 & 0.9940 & 0.9941 & 0.9943 & 0.9945 & 0.9946 & 0.9948 & 0.9949 & 0.9951 & 0.9952 \\ \hline 2.6 & 0.9953 & 0.9955 & 0.9956 & 0.9957 & 0.9959 & 0.9960 & 0.9961 & 0.9962 & 0.9963 & 0.9964 \\ \hline 2.7 & 0.9965 & 0.9966 & 0.9967 & 0.9968 & 0.9969 & 0.9970 & 0.9971 & 0.9972 & 0.9973 & 0.9974 \\ \hline 2.8 & 0.9974 & 0.9975 & 0.9976 & 0.9977 & 0.9977 & 0.9978 & 0.9979 & 0.9979 & 0.9980 & 0.9981 \\ \hline 2.9 & 0.9981 & 0.9982 & 0.9982 & 0.9983 & 0.9984 & 0.9984 & 0.9985 & 0.9985 & 0.9986 & 0.9986 \\ \hline 3.0 & 0.9987 & 0.9987 & 0.9987 & 0.9988 & 0.9988 & 0.9989 & 0.9989 & 0.9989 & 0.9990 & 0.9990 \\ \hline \end{tabular}