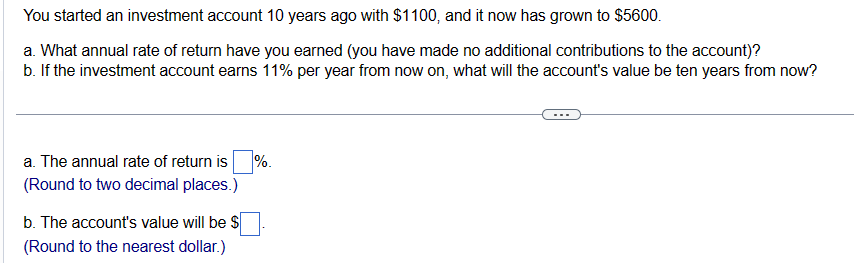
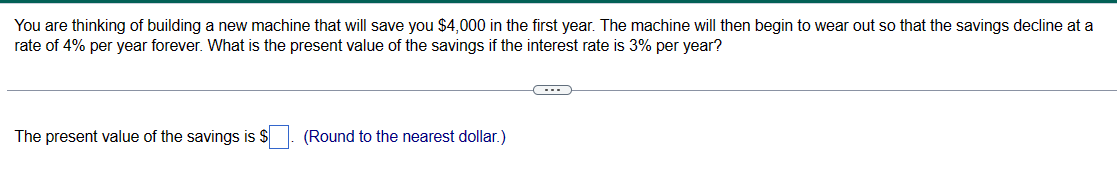
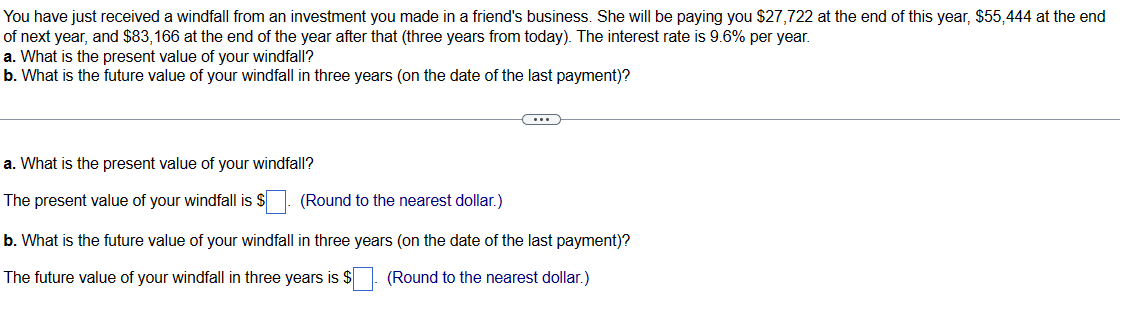
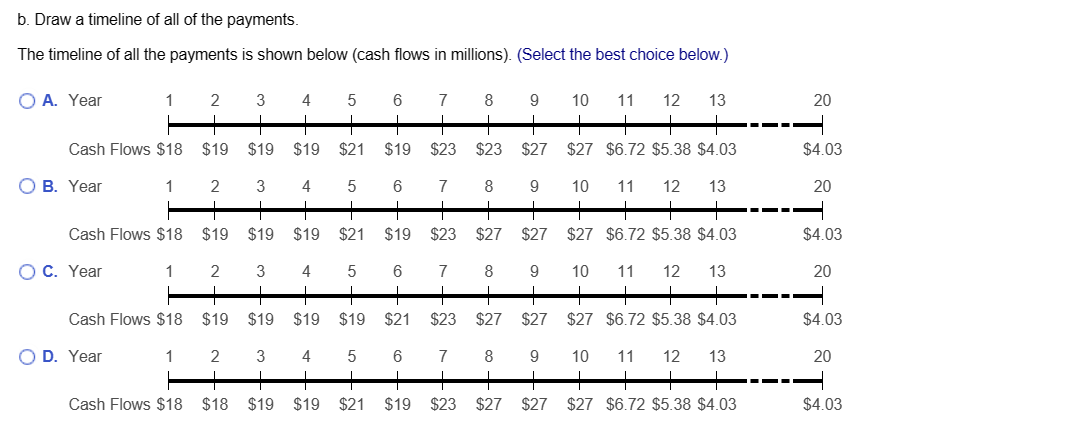
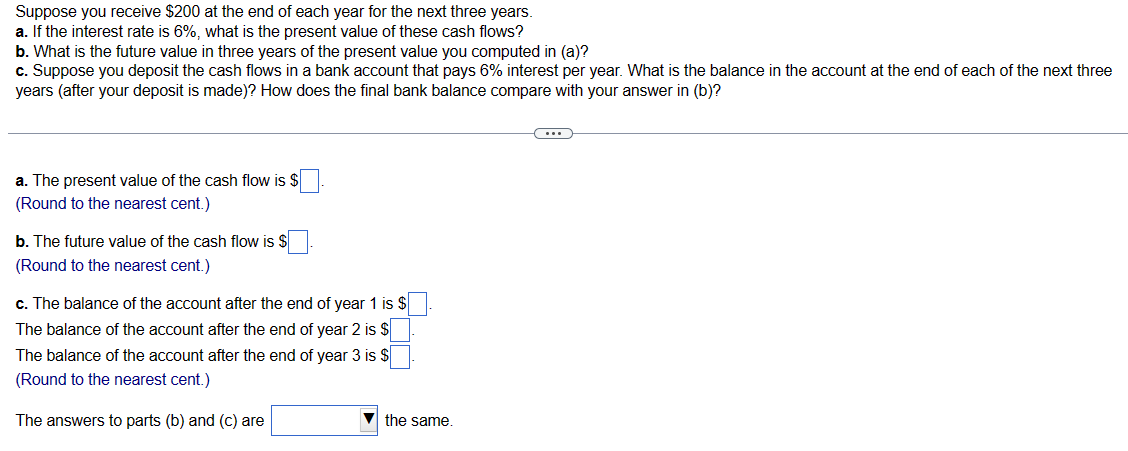
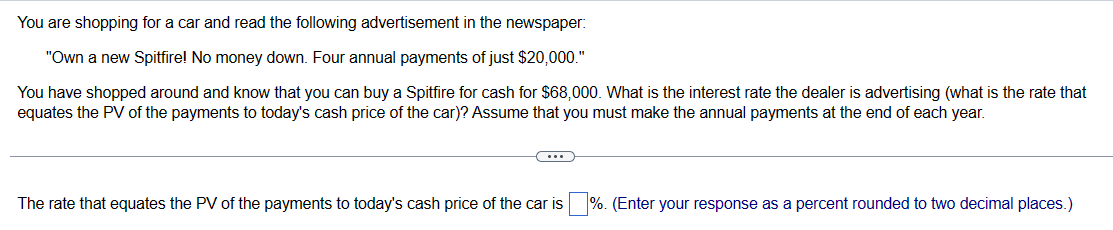
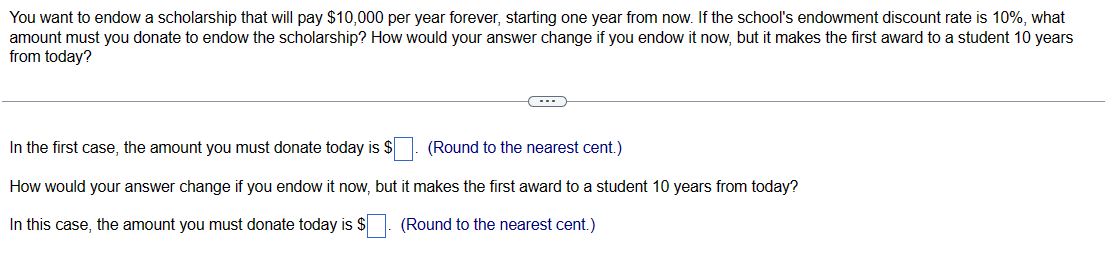
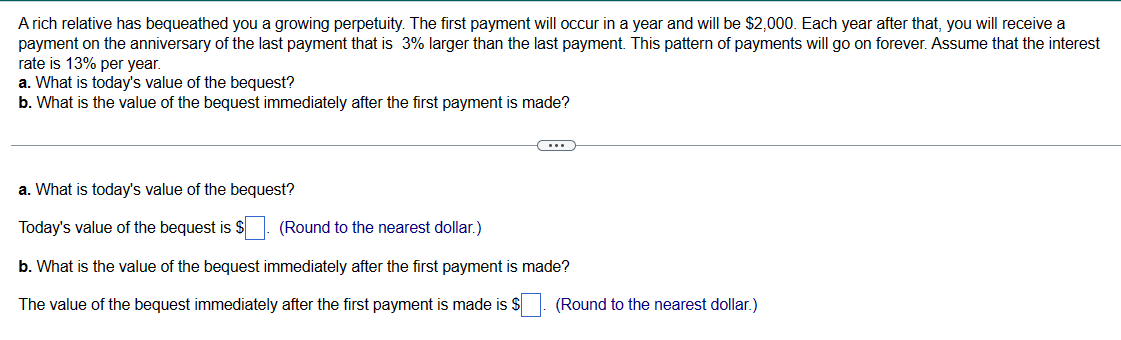
You have decided to buy a perpetual bond. The bond makes one payment at the end of every year forever and has an interest rate of 9%. If the bond initially costs $3,000, what is the payment every year? The payment at the end of each year is $ C---- (Round to the nearest dollar.) You started an investment account 10 years ago with $1100, and it now has grown to $5600. a. What annual rate of return have you earned (you have made no additional contributions to the account)? b. If the investment account earns 11% per year from now on, what will the account's value be ten years from now? a. The annual rate of return is (Round to two decimal places.) b. The account's value will be $ (Round to the nearest dollar.) %. You are thinking of building a new machine that will save you $4,000 in the first year. The machine will then begin to wear out so that the savings decline at a rate of 4% per year forever. What is the present value of the savings if the interest rate is 3% per year? The present value of the savings is $ (Round to the nearest dollar.) ---- You want to endow a scholarship that will pay $11,000 per year forever, starting one year from now. If the school's endowment discount rate is 7%, what amount must you donate to endow the scholarship? The amount you must donate is $ (Round to the nearest cent.) (---) When Alfred Nobel died, he left the majority of his estate to fund five prizes, each to be awarded annually in perpetuity starting one year after he died. (The sixth one, in economics, was added later.) a. If he wanted the cash award of each of the five prizes to be $40,000 and his estate could earn 6% per year, how much would he need to fund his prizes? b. If he wanted the value of each prize to grow by 3% per year (perhaps to keep up with inflation), how much would he need to leave? Assume that the first amount was still $40,000. c. His heirs were surprised by his will and fought it. If they had been able to keep the amount of money you calculated in b and had invested it at 6% per year, how much would they have in 2009, 113 years after he died? a. He would need $ to fund his prizes. (Round to the nearest dollar.) to fund his prizes. b. He would need $ (Round to the nearest dollar.) c. His heirs would have $ (Round to the nearest million.) million. Your grandmother has been putting $3,000 into a savings account on every birthday since your first (that is, when you turned one). The account pays an interest rate of 4%. How much money will be in the account immediately after your grandmother makes the deposit on your 18th birthday? The amount in the account upon your 18th birthday is $ --C--- (Round to the nearest dollar.) The true promised payments under this contract for years 6 through 10 are: (Round all values to the nearest million.) Year 6: $ Year 7: $ Year 8: $ Year 9: $ Year 10: $ million. million. million. million. million. The true promised payments under this contract for years 11 through 20 are: (Round all values to four decimal places.) Year 11: $ million. Year 12: $ million. Years 13 to 20: $ million. You have just received a windfall from an investment you made in a friend's business. She will be paying you $27,722 at the end of this year, $55,444 at the end of next year, and $83,166 at the end of the year after that (three years from today). The interest rate is 9.6% per year. a. What is the present value of your windfall? b. What is the future value of your windfall in three years (on the date of the last payment)? a. What is the present value of your windfall? The present value of your windfall is $ (...) (Round to the nearest dollar.) b. What is the future value of your windfall in three years (on the date of the last payment)? The future value of your windfall in three years is $. (Round to the nearest dollar.) c. Calculate the present value of the contract. The present value of the contract is $ million. (Round to the nearest million.) d. Compare the present value of the contract to the quoted value of $252 million. What explains the difference? (Select the best choice below.) O A. The reason for the difference is that, although the $252 million quoted value does adjust the deferred payments for accrued interest, it does not discount the future cash flows. O B. The reason for the difference is the $252 million quoted value does not discount the future cash flows or adjust deferred payments for accrued interest. O C. The reason for the difference is that, although the $252 million quoted value does discount the future cash flows, it does not adjust the deferred payments for accrued interest. O D. The reason for the difference is that the contract was quoted incorrectly. b. Draw a timeline of all of the payments. The timeline of all the payments is shown below (cash flows in millions). (Select the best choice below.) O A. Year O B. Year 1 O C. Year 2 Cash Flows $18 $19 $19 $19 1 2 4 + $19 $21 Cash Flows $18 1 O D. Year 3 Cash Flows $18 $19 $19 1 3 4 2 3 + + $19 $19 $19 2 3 4 5 4 6 $21 $19 $23 5 7 $19 5 6 $19 5 6 7 $21 6 8 $23 7 $23 8 9 $27 8 $27 $23 $27 $27 7 8 9 9 $27 9 10 11 12 13 $27 $6.72 $5.38 $4.03 10 11 12 13 + $27 $6.72 $5.38 $4.03 10 11 12 13 + + $27 $6.72 $5.38 $4.03 10 11 12 13 Cash Flows $18 $18 $19 $19 $21 $19 $23 $27 $27 $27 $6.72 $5.38 $4.03 20 $4.03 20 $4.03 20 $4.03 20 $4.03 Your grandmother bought an annuity from Canada Life Insurance Company for $419,708 when she retired. In exchange for the $419,708, Canada Life will pay her $50,000 per year until she dies. The interest rate is 3%. How long must she live after the day she retired to come out ahead (that is, to get more in value than what she paid in)? She must live at least years. (Round up to the nearest whole year.) What is the present value of the following set of cash flows, discounted at 15.6% per year? 2 Year CF 1 $106 - $106 The present value of the cash flow stream is $ C (Round to the nearest cent.) 3 $210 4 - $210 a. What is the present value of the following set of cash flows, discounted at 9.4% per year? Year CF 1 $9 2 $21 3 $33 The present value of the cash flow stream is $ (Round to the nearest cent.) b. What is the present value of the following set of cash flows, discounted at 9.4% per year? Year CF 1 $57 2 $45 O A. The present value in part (b) is lower because the larger cash flows occur sooner. OB. The present value in part (b) is higher because the larger cash flows occur sooner. O C. The present value in part (a) is higher because the larger cash flows occur sooner. O D. The present value in part (a) is lower because the larger cash flows occur sooner. 3 $33 4 $45 4 $21 The present value of the cash flow stream is (Round to the nearest cent.) c. Each set contains the same cash flows ($9, $21, $33, $45, $57), so why is the present value different? (Select the best choice below.) 5 $57 5 $9 Suppose you receive $200 at the end of each year for the next three years. a. If the interest rate is 6%, what is the present value of these cash flows? b. What is the future value in three years of the present value you computed in (a)? c. Suppose you deposit the cash flows in a bank account that pays 6% interest per year. What is the balance in the account at the end of each of the next three years (after your deposit is made)? How does the final bank balance compare with your answer in (b)? a. The present value of the cash flow is $ (Round to the nearest cent.) b. The future value of the cash flow is $ (Round to the nearest cent.) c. The balance of the account after the end of year 1 is $ The balance of the account after the end of year 2 is $ The balance of the account after the end of year 3 is $ (Round to the nearest cent.) The answers to parts (b) and (c) are the same. You are shopping for a car and read the following advertisement in the newspaper: "Own a new Spitfire! No money down. Four annual payments of just $20,000." You have shopped around and know that you can buy a Spitfire for cash for $68,000. What is the interest rate the dealer is advertising (what is the rate that equates the PV of the payments to today's cash price of the car)? Assume that you must make the annual payments at the end of each year. C... The rate that equates the PV of the payments to today's cash price of the car is %. (Enter your response as a percent rounded to two decimal places.) You want to endow a scholarship that will pay $10,000 per year forever, starting one year from now. If the school's endowment discount rate is 10%, what amount must you donate to endow the scholarship? How would your answer change if you endow it now, but it makes the first award to a student 10 years from today? C--- In the first case, the amount you must donate today is $. (Round to the nearest cent.) How would your answer change if you endow it now, but it makes the first award to a student 10 years from today? In this case, the amount you must donate today is $ (Round to the nearest cent.) A rich aunt has promised you $3,000 one year from today. In addition, each year after that, she has promised you a payment (on the anniversary of the last payment) that is 1% larger than the last payment. She will continue to show this generosity for 20 years, giving a total of 20 payments. If the interest rate is 8%, what is her promise worth today? The present value of the aunt's promise is $ C... (Round to the nearest dollar.) d. If, instead, you decide to withdraw $40,000 per year in retirement (again with the first withdrawal one year after retiring), how many years will it take until you exhaust your savings? You will exhaust your savings in years. (Round to two decimal places.) e. Assuming the most you can afford to save is $1,600 per year, but you want to retire with $1,000,000.00 in your investment account, how high of a return do you need to earn on your investments? You will need a return of %. (Round to two decimal places.) A rich relative has bequeathed you a growing perpetuity. The first payment will occur in a year and will be $2,000. Each year after that, you will receive a payment on the anniversary of the last payment that is 3% larger than the last payment. This pattern of payments will go on forever. Assume that the interest rate is 13% per year. a. What is today's value of the bequest? b. What is the value of the bequest immediately after the first payment is made? (..) a. What is today's value of the bequest? Today's value of the bequest is $ (Round to the nearest dollar.) b. What is the value of the bequest immediately after the first payment is made? The value of the bequest immediately after the first payment is made is $ (Round to the nearest dollar.) You are trying to decide how much to save for retirement. Assume you plan to save $8,000 per year with the first investment made one year from now. You think you can earn 5% per year on your investments and you plan to retire in 34 years, immediately after making your last $8,000 investment. a. How much will you have in your retirement account on the day you retire? b. If, instead of investing $8,000 per year, you wanted to make one lump-sum investment today for your retirement that will result in the same retirement saving, how much would that lump sum need to be? c. If you hope to live for 30 years in retirement, how much can you withdraw every year in retirement (starting one year after retirement) so that you will just exhaust your savings with the 30th withdrawal (assume your savings will continue to earn 5% in retirement)? d. If, instead, you decide to withdraw $40,000 per year in retirement (again with the first withdrawal one year after retiring), how many years will it take until you exhaust your savings? e. Assuming the most you can afford to save is $1,600 per year, but you want to retire with $1,000,000.00 in your investment account, how high of a return do you need to earn on your investments? (---) a. How much will you have in your retirement account on the day you retire? The amount in the retirement account in 34 years would be $. (Round to the nearest cent.) b. If, instead of investing $8,000 per year, you wanted to make one lump-sum investment today for your retirement that will result in the same retirement saving, how much would that lump sum need to be? You will need to make one lump sum investment today of $. (Round to the nearest cent.) c. If you hope to live for 30 years in retirement, how much can you withdraw every year in retirement (starting one year after retirement) so that you will just exhaust your savings with the 30th withdrawal (assume your savings will continue to earn 5% in retirement)? The amount you can withdraw every year in retirement is $. (Round to the nearest cent.) When Alex Rodriguez moved to the Texas Rangers in 2001, he received a lot of attention for his "$252 million" contract (the total of the payments promised was $252 million). Assume the following about the contract. Rodriguez earns $16 million in the first year, $17 million in years 2 through 4, $19 million in years 5 and 6, $23 million in year 7, and $27 million in years 8 through 10. He would also receive his $10 million signing bonus spread equally over the first 5 years ($2 million per year). His deferred payments begin in 2011. The deferred payment amounts total $33 million and are $5 million, then $4 million, then eight amounts of $3 million (ending in 2020). However, the actual payouts will be different. All of the deferred payments will earn 3% per year until they are paid. For example, the $5 million is deferred from 2001 to 2011, or 10 years, meaning that it will actually be $6.7196 million when paid. Assume that the $4 million payment deferred to 2012 is deferred from 2002 (each payment is deferred 10 years). The contract is a 10-year contract, but each year has a deferred component so that cash flows are paid out over a total of 20 years. The contractual payments, signing bonus, and deferred components are given below. Note that, by contract, the deferred components are not paid in the year they are earned but instead are paid (plus interest) 10 years later. a. Calculate the true promised payments under this contract, including the deferred payments with interest. The true promised payments under this contract for years 1 through 5 are: (Round all values to the nearest integer.) Year 1: $ Year 2: $ Year 3: $ Year 4: $ Year 5: $ million. million. million. million. million.