





 you need this for the question number 3 please
you need this for the question number 3 please
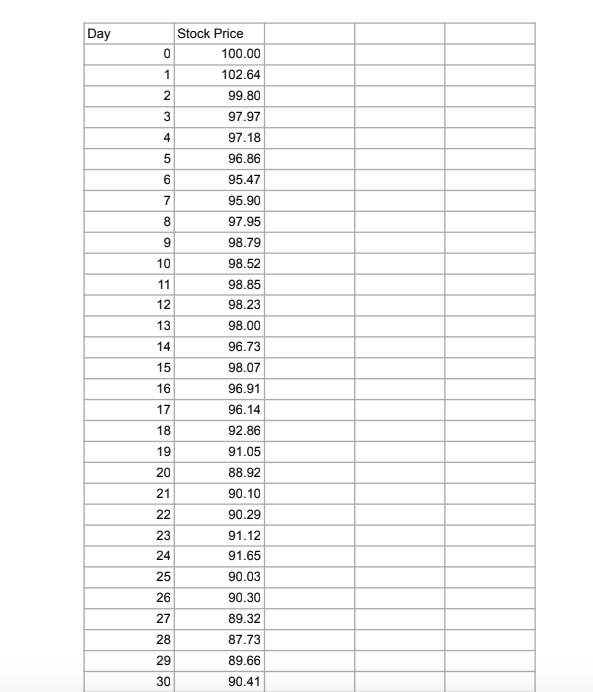
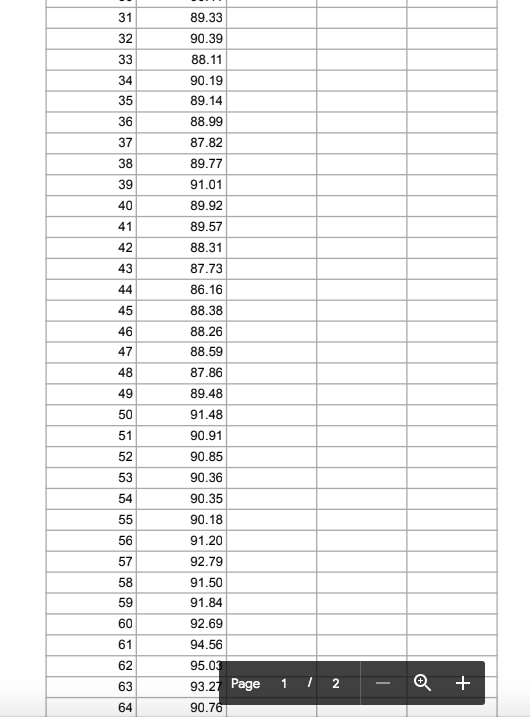
Q1) Given the following inputs: TCAD 0.50% PETUSD 0.40% Spot USD/CAD 1.30 Sigma 10% T(months) Option Type Call a) What is the T month forward USD/CAD exchange rate? b) Use the Black-Scholes formula to compute the price of a T month, at the money European style option of the type specified (put or call) on $1 million USD. (That is, the right to sell (put) / buy (call) $1 million USD and receive (puty/pay (call) the Spot(USD/CAD) * 1 million CAD.) Is the buyer of this option hoping that the US dollar will go up or down relative to the Canadian dollar? c) Compute the values for u, d, pup, pdn and use them to construct a 2 step, a 4 step, and a 10 step binomial tree, and then price the European option using each of these trees. Compare your answers to the answer you got using Black-Scholes. Do they get better as the number of time steps in the tree increase? d) Assume the option is American style instead of European style. Build 2 step, 4 step, and 10 step binomial trees to price the option. e) Assume the option is Bermuda style, with possible exercise times of T/2 and T. Build 2 step, 4 step, and 10 step binomial trees to price the option. f) We know that American style >= Bermuda style >= European style. If, using the given inputs, you get the same value for any two of these, change ra and/or rf (within reason, i.e. 20% > rd, rf > 0) and see if you can get different answers for all three (Am style > Berm style > Euro style). What ra and rf work for you? Why? Q2) Given the following inputs for TFS: 5.00% delta (div rate) 2.00% Spot 100 Strike 105 Sigma 40% T(months) Option Type Put a) Use the Black-Scholes formula to compute the price for the given option. Graph the payoff and profit diagrams, computing all key points. b) Suppose the bid price of the option is $0.10 less than the option price from a). Find the implied volatility corresponding to this price. This is called the bid volatility. Do the same for the ask volatility assuming the ask price is $0.10 more than the option price from a). c) Assume the stock price increases by 10%. Compute the new option price (using the input volatility). Compute the new bid/ask prices for the option using the bid/ask volatilities from b). Do the same if the stock price decrease by 10%. d) Are the new bid/ask spreads (prices) roughly the same as the initial bid/ask spread? Are the new option prices roughly in the middle of the new bid/ask spreads? Do you see why option market makers think in terms of volatilities (which change slowly) instead of prices (which change quickly)? e) Find Delta for the original option at the original spot price, and construct the delta hedged portfolio. Graph the payoff and profit diagrams, computing all key points. f) (Hard!) Show that the delta hedged portfolio has the exact same profit and payoff as an asymmetric straddle (long n1 puts, long n2 calls both at the same strike as the original option - you must find n1 and n2). Can you explain why / prove it using Put Call Parity? Q3) See the first page of the spreadsheet "Q3 Data" with 3 months (30 days/month) of price data for TFS. a) Fill in the column Daily Returns" with the continuously compounded) daily return. b) Compute the annualized historical volatility based on this data. c) Price a 1 month (30 day) at-the-money European call option using the Black-Scholes formula and the following inputs: 5.00% 2.00% delta (div rate) Elias thinks the stock is going up over the next month so he buys the at-the-money call option from the market maker Angela. Elias doesn't delta hedge and simply waits until the end of 30 days to see if he makes or loses money. Angela has no opinion on whether the stock will go up or down so she immediately delta hedges her option position. The prices on the second page of "Q3 Data" are the stock prices over the 30 day lifetime of the option. d) Does Elias make or lose money? e) Fill in the column "Daily Returns" with the (continuously compounded) daily return. Compute the realized volatility (annualized) from this data. Comparing this with your answer to b) do you expect Angela to make or lose money? f) Assume Angela rebalances her delta hedge every 6 days. (i.e she delta hedges the option when she sells it, and she rebalances her delta hedge at the end of days 6,12,18, and 24, and closes out her position at the end of day 30.) What is her P&L (profit or loss) when the option expires? g) Is it possible for Elias and Angela to both make (or both lose) money? Day Stock Price 100.00 102.64 99.80 97.97 97.18 96.86 95.47 95.90 97.95 98.79 98.52 98.85 98.23 98.00 96.73 98.07 96.91 96.14 92.86 91.05 88.92 90.10 90.29 91.12 91.65 90.03 90.30 89.32 87.73 89.66 90.41 89.33 90.39 88.11 90.19 89.14 88.99 87.82 89.77 91.01 89.92 89.57 88.31 87.73 86.16 88.38 88.26 88.59 87.86 89.48 91.48 90.91 90.85 90.36 90.35 90.18 91.20 92.79 91.50 91.84 92.69 94.56 95.03 93.27 Page 1 90.76 62 63 2 - + 64 Q1) Given the following inputs: TCAD 0.50% PETUSD 0.40% Spot USD/CAD 1.30 Sigma 10% T(months) Option Type Call a) What is the T month forward USD/CAD exchange rate? b) Use the Black-Scholes formula to compute the price of a T month, at the money European style option of the type specified (put or call) on $1 million USD. (That is, the right to sell (put) / buy (call) $1 million USD and receive (puty/pay (call) the Spot(USD/CAD) * 1 million CAD.) Is the buyer of this option hoping that the US dollar will go up or down relative to the Canadian dollar? c) Compute the values for u, d, pup, pdn and use them to construct a 2 step, a 4 step, and a 10 step binomial tree, and then price the European option using each of these trees. Compare your answers to the answer you got using Black-Scholes. Do they get better as the number of time steps in the tree increase? d) Assume the option is American style instead of European style. Build 2 step, 4 step, and 10 step binomial trees to price the option. e) Assume the option is Bermuda style, with possible exercise times of T/2 and T. Build 2 step, 4 step, and 10 step binomial trees to price the option. f) We know that American style >= Bermuda style >= European style. If, using the given inputs, you get the same value for any two of these, change ra and/or rf (within reason, i.e. 20% > rd, rf > 0) and see if you can get different answers for all three (Am style > Berm style > Euro style). What ra and rf work for you? Why? Q2) Given the following inputs for TFS: 5.00% delta (div rate) 2.00% Spot 100 Strike 105 Sigma 40% T(months) Option Type Put a) Use the Black-Scholes formula to compute the price for the given option. Graph the payoff and profit diagrams, computing all key points. b) Suppose the bid price of the option is $0.10 less than the option price from a). Find the implied volatility corresponding to this price. This is called the bid volatility. Do the same for the ask volatility assuming the ask price is $0.10 more than the option price from a). c) Assume the stock price increases by 10%. Compute the new option price (using the input volatility). Compute the new bid/ask prices for the option using the bid/ask volatilities from b). Do the same if the stock price decrease by 10%. d) Are the new bid/ask spreads (prices) roughly the same as the initial bid/ask spread? Are the new option prices roughly in the middle of the new bid/ask spreads? Do you see why option market makers think in terms of volatilities (which change slowly) instead of prices (which change quickly)? e) Find Delta for the original option at the original spot price, and construct the delta hedged portfolio. Graph the payoff and profit diagrams, computing all key points. f) (Hard!) Show that the delta hedged portfolio has the exact same profit and payoff as an asymmetric straddle (long n1 puts, long n2 calls both at the same strike as the original option - you must find n1 and n2). Can you explain why / prove it using Put Call Parity? Q3) See the first page of the spreadsheet "Q3 Data" with 3 months (30 days/month) of price data for TFS. a) Fill in the column Daily Returns" with the continuously compounded) daily return. b) Compute the annualized historical volatility based on this data. c) Price a 1 month (30 day) at-the-money European call option using the Black-Scholes formula and the following inputs: 5.00% 2.00% delta (div rate) Elias thinks the stock is going up over the next month so he buys the at-the-money call option from the market maker Angela. Elias doesn't delta hedge and simply waits until the end of 30 days to see if he makes or loses money. Angela has no opinion on whether the stock will go up or down so she immediately delta hedges her option position. The prices on the second page of "Q3 Data" are the stock prices over the 30 day lifetime of the option. d) Does Elias make or lose money? e) Fill in the column "Daily Returns" with the (continuously compounded) daily return. Compute the realized volatility (annualized) from this data. Comparing this with your answer to b) do you expect Angela to make or lose money? f) Assume Angela rebalances her delta hedge every 6 days. (i.e she delta hedges the option when she sells it, and she rebalances her delta hedge at the end of days 6,12,18, and 24, and closes out her position at the end of day 30.) What is her P&L (profit or loss) when the option expires? g) Is it possible for Elias and Angela to both make (or both lose) money? Day Stock Price 100.00 102.64 99.80 97.97 97.18 96.86 95.47 95.90 97.95 98.79 98.52 98.85 98.23 98.00 96.73 98.07 96.91 96.14 92.86 91.05 88.92 90.10 90.29 91.12 91.65 90.03 90.30 89.32 87.73 89.66 90.41 89.33 90.39 88.11 90.19 89.14 88.99 87.82 89.77 91.01 89.92 89.57 88.31 87.73 86.16 88.38 88.26 88.59 87.86 89.48 91.48 90.91 90.85 90.36 90.35 90.18 91.20 92.79 91.50 91.84 92.69 94.56 95.03 93.27 Page 1 90.76 62 63 2 - + 64







 you need this for the question number 3 please
you need this for the question number 3 please 





