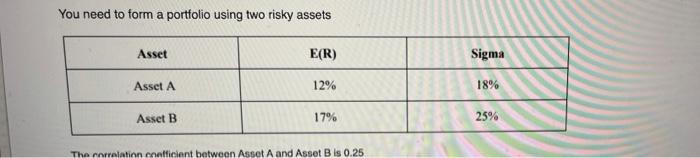
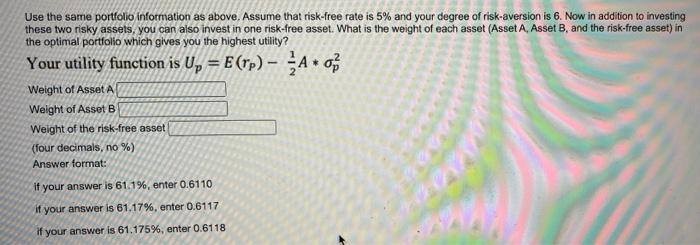
You need to form a portfolio using two risky assets Asset E(R) Sigma Asset A 12% 18% Asset B 17% 25% The relation netficient between Asset A and Asset B is 0.25 Use the same portfolio information as above, what is the weight of asset in the minimum variance portfolio? (four decimals, no %) Answer format if your answer is 61.1%, enter 0.6110 if your answer is 61.17%, enter 0.6117 if your answer is 61.175%, enter 0.6118 Use the same portfolio information as above. Assume that risk-free rate is 5% and your degree of risk-aversion is 6. Now in addition to investing these two risky assets, you can also invest in one risk-free asset. What is the weight of each asset (Asset A, Asset B, and the risk-free asset) in the optimal portfolio which gives you the highest utility? Your utility function is Up = E(rp) A of Weight of Asset A Weight of Asset B Weight of the risk-free asset (four decimals, no %) Answer format: if your answer is 61.1%, enter 0.6110 if your answer is 61.17%, enter 0.6117 if your answer is 61.175%, enter 0.6118 Use the same portfolio information as above. Assume that your degree of risk aversion increase to 8. Then, in the risky. portfolio which has the highest sharp ratio (the tangency portfolio), the weight of asset A will in other words, should the answer in Q7 change)? Increase Decrease The weight of asset A and asset B will stay the same The weight of asset A will change. However, there is not enough information to decide whether the weight will increase or decrease. Use the same portfolio information as above. Assume that your degree of risk aversion increase to 8. Then, in the optimal portfolio which gives you the highest utility level, the weight of the risk-free asset will O Increase Decrease Stay the same Not enough information to decide You need to form a portfolio using two risky assets Asset E(R) Sigma Asset A 12% 18% Asset B 17% 25% The relation netficient between Asset A and Asset B is 0.25 Use the same portfolio information as above, what is the weight of asset in the minimum variance portfolio? (four decimals, no %) Answer format if your answer is 61.1%, enter 0.6110 if your answer is 61.17%, enter 0.6117 if your answer is 61.175%, enter 0.6118 Use the same portfolio information as above. Assume that risk-free rate is 5% and your degree of risk-aversion is 6. Now in addition to investing these two risky assets, you can also invest in one risk-free asset. What is the weight of each asset (Asset A, Asset B, and the risk-free asset) in the optimal portfolio which gives you the highest utility? Your utility function is Up = E(rp) A of Weight of Asset A Weight of Asset B Weight of the risk-free asset (four decimals, no %) Answer format: if your answer is 61.1%, enter 0.6110 if your answer is 61.17%, enter 0.6117 if your answer is 61.175%, enter 0.6118 Use the same portfolio information as above. Assume that your degree of risk aversion increase to 8. Then, in the risky. portfolio which has the highest sharp ratio (the tangency portfolio), the weight of asset A will in other words, should the answer in Q7 change)? Increase Decrease The weight of asset A and asset B will stay the same The weight of asset A will change. However, there is not enough information to decide whether the weight will increase or decrease. Use the same portfolio information as above. Assume that your degree of risk aversion increase to 8. Then, in the optimal portfolio which gives you the highest utility level, the weight of the risk-free asset will O Increase Decrease Stay the same Not enough information to decide