You will solve the same exact problem as in Question 1, but, this time you will write a recursive Python function called generate_r( n ) that generates a series or rows of numbers stored as sublists according to the above-mentioned rules.

To help you, a possible algorithm for the task is provided to you below. Intentionally though, not every detail is given in this algorithm, and the details you need to fill in are all about how you must go about implementing each of the steps mentioned in this algorithm.

Algorithm Generate_R( n ): IF n is 1 THEN: RETURN [[1]] ELSE: vv = generate rows for the previous (n - 1) rows pp = grab the last row from vv rr = generate values for the current row using values in pp gg = build/join the entire set of rows from rr and vv RETURN gg

• The implemention below provides a few lines of the implementation of the above algorithm. On the other hand, you have complete freedom as to how you may wish to implement a solution, as long as that solution is recursive!

• The algorithm above and the code snippet below are only suggestions in the right direction. Remember that multiple solutions that satisfy the specifications are possible is no single solution.

• When you run the following cell, a file namd generate_r.py should be created, since a file magic directive is used at the top of the cell. You should not modify this line.

• Again, a function that you write may work. However, if it fails to follow the strict specifications provided to you, unfortunately, you will not get any grade for this question. So, if you do not remember additional specifications about what you are not allowed to do, please refer to Question 1

QUESTION 1:

Write an iterative Python function called generate_i( n ) that generates a series or rows of numbers stored as sublists according to the following rules:

• Start by returning [1] for n=1

• Continue by returning [1, 1] for n=2

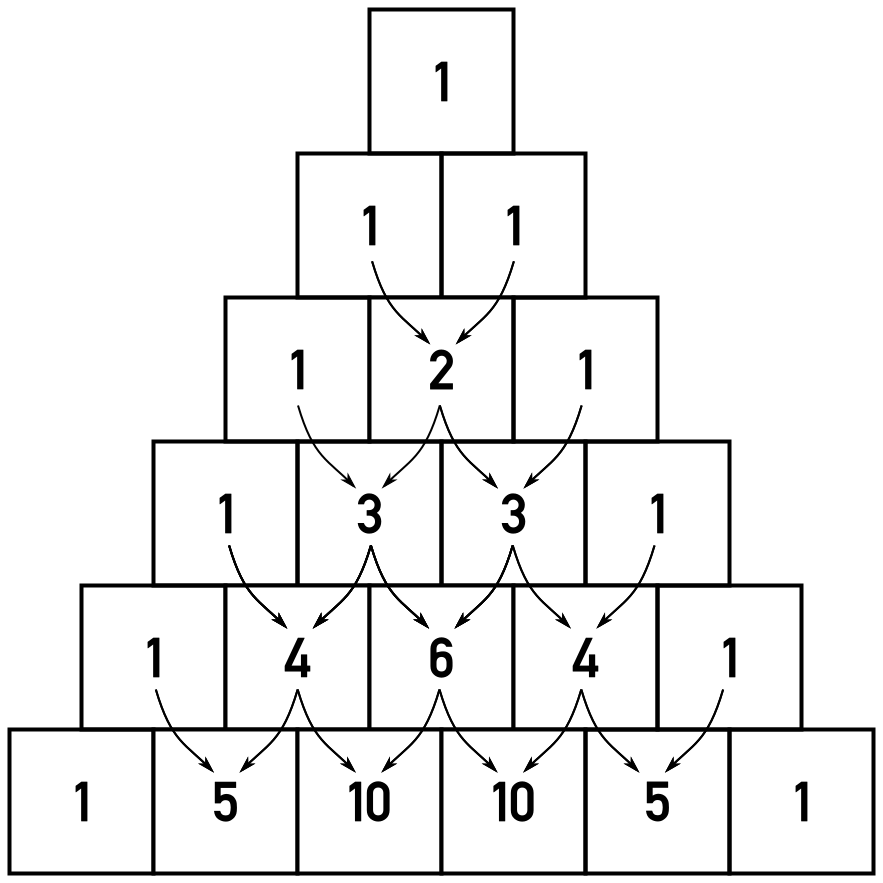
• Each remaining row of values will thus continue to have one more value than the previous row. For example, the fifth row will have five values, while the fourth row has four. The values on both ends of the current row will always be 1 for n > 1. Starting with the second row, each internal cell will be the sum of the two cells diagonally right above that cell.

• Hence, n such rows should be generated by generate_i( n ).

Below is a pictorial description of the values that should be generated with the call generate_i( 6 ):

For example, take the row before last from the bottom. Both ends have 1, as required. The first leftmost value after 1 is 4, because, above it are cells 1 and 3, whose sum is 4. The middle element of the last row to be generated for n=6 is 6, because above it are two 3s.

Your generate_i( n ) function will return a list of lists, in which each sublist will store one of these rows of numbers, starting with 1 at the top. Therefore, the return value of generate_i( 6 ) should be

[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1], [1, 5, 10, 10, 5, 1]] 

where each row is represented by a sublist. So there are 6 sublists for n=6.

• As mentioned above, your generate_i() function must be iterative, that is, it must strictly use looping to do its job.

• You are not allowed to use import statements or the zip() function. If you do, your grade will automatically be zero.

• You are not allowed to define additional functions! So you should only define generate_i() in your solution. If you define additional helperfunctions external or internal to generate_i(), they will be automatically detected, and, unfortunately, your grade will be zero.

• You will use the Jupyter Notebook file magic directive (%%file ...) to store your solution as generate_i.py. Therefore, do not remove this directive from the top of the following code cell

%%file generate_i.py

def generate_i( n ): """ Read above specifications carefully """ # YOUR CODE HERE

pass

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 | 5 10 16 5 1 1