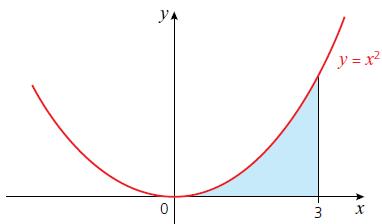
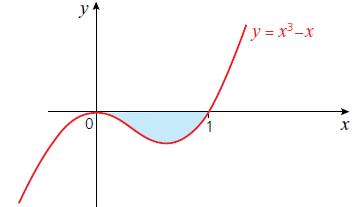
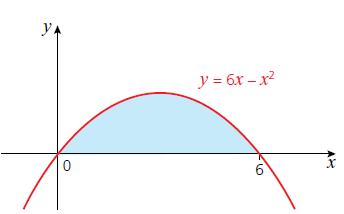
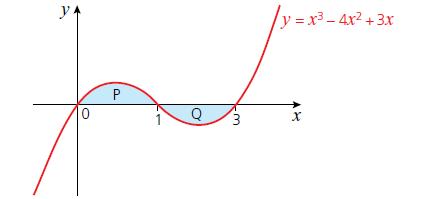
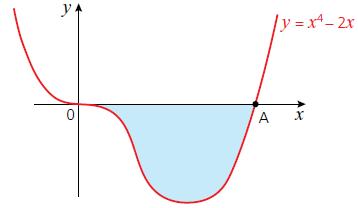
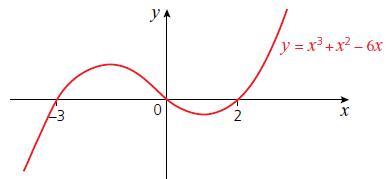
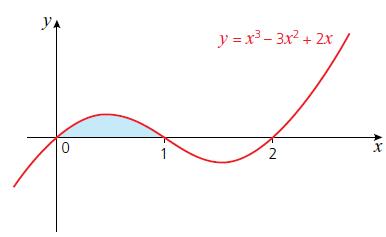
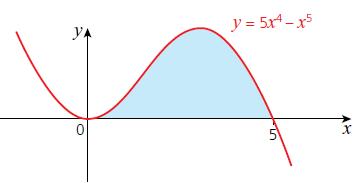
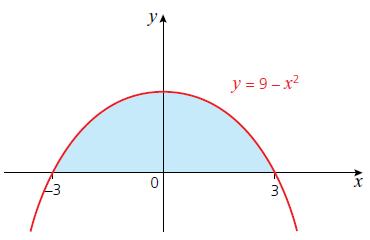
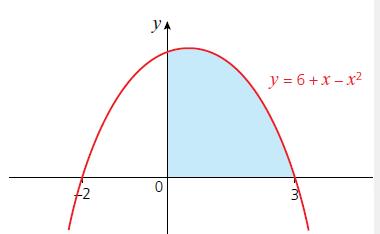
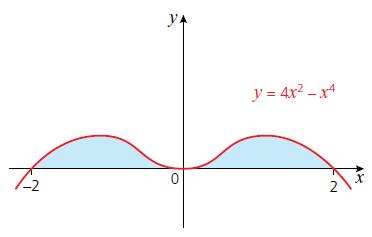
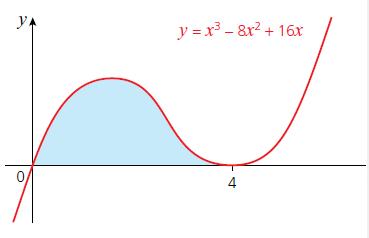
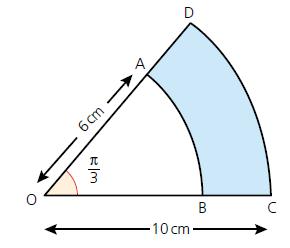
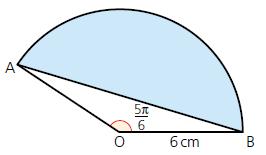
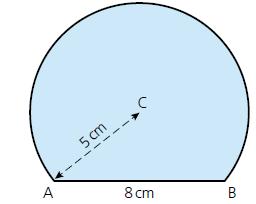
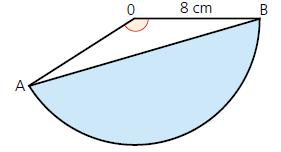
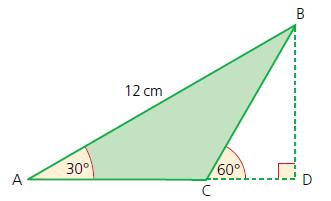
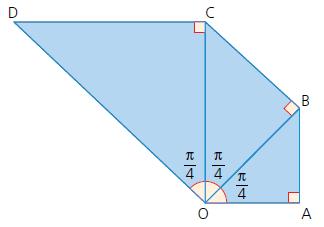
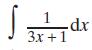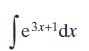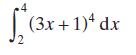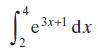Cambridge IGCSE And O Level Additional Mathematics 1st Edition Val Hanrahan, Jeanette Powell - Solutions

Discover comprehensive solutions for "Cambridge IGCSE and O Level Additional Mathematics 1st Edition" by Val Hanrahan and Jeanette Powell. Access online resources with an extensive answers key, offering detailed solutions in a solution manual format. Explore solutions in PDF for easy reference, featuring solved problems and questions with answers. Dive into the test bank for in-depth chapter solutions and step-by-step answers, ideal for both students and instructors. This instructor manual complements your textbook, enhancing your understanding. Enjoy the convenience of free download options for seamless learning.