Determine the parametric dependence of eddy length in (17-102) and mixing time in (17-103) for the tee-mixer in Figure 17.41, summarized in the following general expressions:

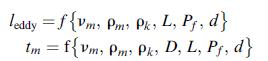
The pressures and velocities in each jet will be matched, with velocity being uniquely determined by parameters in the general expression. Begin with Bernoulli’s equation:

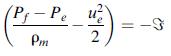
where P represents the pressure in Pascals, with subscripts f and e for feed and exit conditions, respectively; ue is the exit velocity of the mixed stream; and d is the pipe diameter in m. The friction loss З in the system, = in m²/s², is given [50] by:

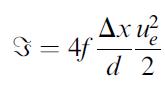
where Δx is the length, L, over which the pressure drop occurs plus equivalent lengths, L_e/d, that account for pressure drop through fittings,

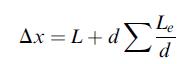
and friction factor, f, is given by

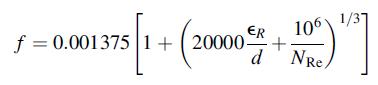
where ϵ_R is the pipe roughness in m, which ranges from 10 to 10°6 m. This equation is applicable for NRe > 4;000. Values of equivalent length range from Le/d = 2 for a union up to 350 for a globe valve. Mixture kinematic viscosity may be estimated using he Refutas equation [51]:

where VBN is the viscosity blending number of the mixture, given by:

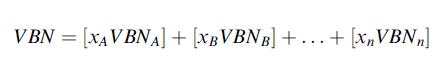
with x_n being the mass fraction of each of the components. Component VBN values are found by inverting the Refutas equation.

Transcribed Image Text:

leddy = f {vm, Pms Pk, L, Pj, d} tm = f{vm, Pms Pks D, L, Pf, d}