Consider the application of the DTFT properties to filters.

(a) Let h[n]be the impulse response of an ideal low-pass filter with  frequency response

If we let the impulse response of a new filter be h₁[n]= [1 + ( ˆ’ 1)ⁿ] h[n],  find the frequency response H₁(e^jω) in terms of H(e^jω). What type of filter  is the new filter?

(b) Consider the frequency response of a filter

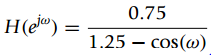
i. From H(e^jω) find the sum

ii. Given that H(e^jω) = H(e ^ˆ’jω), i.e., it is real and an even function of ω, show that h[n] is an even function of n. Use the  inverse DTFT definition.

iii. Is it true that the phase response ˆ H(e^jω) is zero for all discrete frequencies? Explain.

Transcribed Image Text:

1 -0.47 < w < 0.4M 0 otherwise in (–x,7] H(e") = но H(e) 0.75 1.25 – cos(@)