Consider the following problems related to LTI systems.

(a) The impulse response of an FIR filter is h[n]= αⁿ(u[n] ˆ’ u[n ˆ’ M])

i. Is it true that the transfer function for the filter is

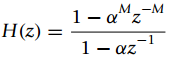
for any value of α?

ii. Let M = 3, 0 ‰¤ α < 1, write H(z) as a polynomial, and then show that it equals

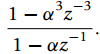
Determine the region of convergence of H(z).

(b) Consider the two-sided impulse response h[n] = 0.5^|n|, ˆ’ (N ˆ’ 1) ‰¤ n ‰¤ N ˆ’ 1.

i. Determine the causal impulse response h₁[n], so that h[n] = h₁[n] + h₁[ ˆ’ n]

ii. Let N = 4, find the transfer function H(z) using the transfer function H₁[z], and determine the region of convergence of H(z) using the ROC of H₁(z).

iii. Let N †’ ˆž, find the transfer function H(z) and its ROC.

(c) Given the finite length impulse response h[n] = 0.5n(u[n] ˆ’ u[n ˆ’ 2]).

i. Find the Z-transforms of the even, h_e[n], and the odd, h_o[n], components of h[n].

ii. Determine the regions of convergence of the Z-transforms of h_e[n] and h_o[n]. How would the region of convergence of H(z) be obtained from the ROCs of X_e(z) and X_o(z)? Explain. Find h_e[n] and h_o[n].

Transcribed Image Text:

1-αz M_-M Н(2) -1 1-αz 3 -3 1-α'z -1 1-αz