Consider the following problems related to filtering of periodic signals:

(a) A periodic signal x(t)of fundamental frequency Ω₀ = Ï€/4 is the input of an ideal band-pass filter with the following frequency response

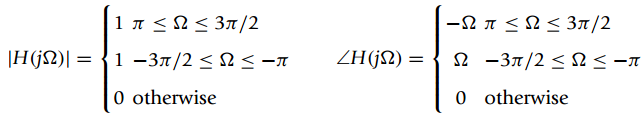
The non-zero Fourier series coefficients of x(t)are

X₁ = X^ˆ—_ˆ’1 = j, X₅ =X^ˆ—_ˆ’5 =2.

i.Express x(t) in the form

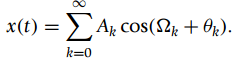
ii. Find the output y(t) of the ideal band-pass filter.

(b) The Fourier series of a periodic signal x(t) is

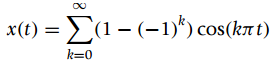
If x(t) is filtered with a filter having the following frequency response

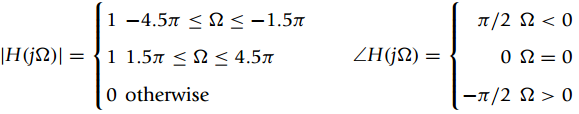
i. Carefully plot the frequency response, magnitude, and phase, of the filter and determine the type of filter it is.

ii. Calculate the steady-state response y_ss(t)of the filter for the given input.

Transcribed Image Text:

1π<Ω < 3π/2 -2 I