Suppose you are given the observer space representation with matrix and vectors

To find a transformation that diagonalizes A_o use MATLAB function eigswhich calculates the eigenvalues and eigenvectors corresponding to the matrix and allows us to express

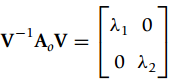
where V is a matrix created with the eigenvectors and {λ_i}, i = 1, 2, are the eigenvalues.

(a) Find the characteristic equation

det(sIˆ’ A_o)

corresponding to the state-variable representation, and show it is the same as the denominator of the transfer function (use function ss2tf to obtain the transfer function from the state-variable representation).

(b) Use the matrix V as an invertible transform to obtain a new set of state variables with a diagonal matrix A and vectors b and c^T. Obtain these matrix and vectors.

(c) Suppose that you find the controller form by letting A_c = A^T_o, b_c = c^T_o, and c^T_c = b^T₀, repeat the above diagonalization and comment on your results.

BI ,d = [1 ] -11 ,bo A, -1 2 0 || || λ1 0 v'A,V = 0 λ