Suppose you wish to find the area under a signal x(t) using sums. You will need the following result found above

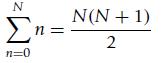
(a) Consider first x(t) = t, 0 ≤ t ≤ 1, and zero otherwise. The area under this signal is 0.5. The integral can be approximated from above and below as

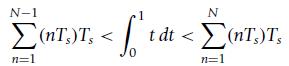
where NT_s = 1 (i.e., we divide the interval [0, 1] into N intervals of width T_s). Graphically show for N = 4 that the above equation makes sense by showing the right and left bounds as approximations for the area under x(t).

(b) Let T_s = 0.001, use the symbolic function symsum to compute the left and right bounds for the above integral. Find the average of these results and compare it with the actual value of the integral.

(c) Verify the symbolic results by finding the sums on the left and the right of the above inequality using the summation given at the beginning of the problem. What happens when N → ∞.

(d) Write a MATLAB script to compute the area under the signal y(t) = t² from 0 ≤ t ≤ 1. Let T_s = 0.001. Compare the average of the lower and upper bounds to the value of the integral.

Transcribed Image Text:

N(N + 1) En= 2 n=0