The Fourier transforms of even and odd functions are very important. Let x(t) = e^??t? and y(t) = e^?t u(t) ? e^t u(?t).

(a) Plot x(t) and y(t), and determine whether they are even or odd.

(b) Show that the Fourier transform of x(t) is found from

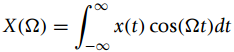
which is real function of ??, therefore its computational importance. Show that X(?) is an even function of ?. Find X(?) from the above equation (called the cosine transform).

(c) Show that the Fourier transform of y(t) is found from

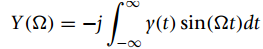
which is imaginary function of ??, thus its computational importance. Show that Y(?) is and odd function of ??. Find Y(?)from the above equation (called the sine transform). Verify that your results are correct by finding the Fourier transform of z(t) = x(t) + y(t) directly and using the above results.

(d) What advantages do you see in using the cosine and sine transforms? How would you use the cosine and the sine transforms to compute the Fourier transform of any signal, not necessarily even or odd? Explain.

Transcribed Image Text:

X(2) x(t) cos(2t)dt